  | Lee, C.-K., Mihai, L. A., Kerfriden, P., & BORDAS, S. (In press). The edge-based strain smoothing method for compressible and nearly incompressible non-linear elasticity for solid mechanics. ORBilu-University of Luxembourg. https://orbilu.uni.lu/handle/10993/14933. |
  | CHEN, L., Berke, P., Massart, T., BEEX, L., Magliulo, M., & BORDAS, S. (In press). A refinement indicator for adaptive quasicontinuum approaches for structural lattices. International Journal for Numerical Methods in Engineering. doi:10.1002/nme.6629  Peer Reviewed verified by ORBi |
  | PAPAVASILEIOU, P., Giovanis, D. G., POZZETTI, G., Kathrein, M., Czettl, C., Kevrekidis, I. G., Boudouvis, A. G., BORDAS, S., & KORONAKI, E. (January 2025). Integrating supervised and unsupervised learning approaches to unveil critical process inputs. Computers and Chemical Engineering, 192, 108857. doi:10.1016/j.compchemeng.2024.108857 Peer reviewed |
 | SKY, A., HALE, J., ZILIAN, A., BORDAS, S., & Neff, P. (01 December 2024). Intrinsic mixed-dimensional beam-shell-solid couplings in linear Cosserat continua via tangential differential calculus. Computer Methods in Applied Mechanics and Engineering, 432 (A), 117384. doi:10.48550/arXiv.2407.12515 Peer Reviewed verified by ORBi |
 | SHEN, Z., SOSA, R. I., BORDAS, S., TKATCHENKO, A., & LENGIEWICZ, J. (01 November 2024). Quantum-informed simulations for mechanics of materials: DFTB+MBD framework. International Journal of Engineering Science, 204, 104126. doi:10.1016/j.ijengsci.2024.104126 Peer Reviewed verified by ORBi |
 | PAPAVASILEIOU, P., FARINA, S., KORONAKI, E., BOUDOUVIS, A., BORDAS, S., & SKUPIN, A. (2024). Machine Learning-based Predictions of Spatial Metabolic Profiles Demonstrate the Impact of Morphology on Astrocytic Energy Metabolism. (preprint). ORBilu-University of Luxembourg. https://orbilu.uni.lu/handle/10993/62074. doi:10.1101/2024.09.18.613725 |
 | DESHPANDE, S., RAPPEL, H., Hobbs, M., BORDAS, S., & Lengiewicz, J. (2024). Gaussian process regression + deep neural network autoencoder for probabilistic surrogate modeling in nonlinear mechanics of solids. ORBilu-University of Luxembourg. https://orbilu.uni.lu/handle/10993/61242. |
 | Montorsi, C., FUSCO, A., VAN KERM, P., & BORDAS, S. (November 2023). Predicting depression in old age: Combining life course data with machine learning. Economics and Human Biology, 52, 101331. doi:10.1016/j.ehb.2023.101331 Peer Reviewed verified by ORBi |
 | FARINA, S., VOORSLUIJS, V., FIXEMER, S., BOUVIER, D., Claus, S., Ellisman, M. H., BORDAS, S., & SKUPIN, A. (20 September 2023). Mechanistic multiscale modelling of energy metabolism in human astrocytes reveals the impact of morphology changes in Alzheimer's Disease. PLoS Computational Biology, 19 (9), 1011464. doi:10.1371/journal.pcbi.1011464 Peer Reviewed verified by ORBi |
 | MAZIER, A., El Hadramy, S., Brunet, J.-N., HALE, J., Cotin, S., & BORDAS, S. (2023). SOniCS: Develop intuition on biomechanical systems through interactive error controlled simulations. Engineering with Computers. doi:10.1007/s00366-023-01877-w Peer Reviewed verified by ORBi Dataset: 10.6084/m9.figshare.21120118 |
 | VIJAYARAGHAVAN, S., Wu, L., Noels, L., BORDAS, S., Natarajan, S., & BEEX, L. (07 August 2023). A data-driven reduced-order surrogate model for entire elastoplastic simulations applied to representative volume elements. Scientific Reports, 13 (1), 12781. doi:10.1038/s41598-023-38104-x Peer Reviewed verified by ORBi Dataset: 10.1038/s41598-023-38104-x |
 | PAPAVASILEIOU, P., KORONAKI, E., POZZETTI, G., Kathrein, M., Czettl, C., Boudouvis, A. G., & BORDAS, S. (August 2023). Equation-based and data-driven modeling strategies for industrial coating processes. Computers in Industry, 149, 103938. doi:10.1016/j.compind.2023.103938 Peer Reviewed verified by ORBi |
 | DESHPANDE, S., SOSA, R. I., BORDAS, S., & LENGIEWICZ, J. (August 2023). Novel deep learning approaches for learning scientific simulations [Paper presentation]. The 14th International Conference of Computational Methods (ICCM2023), Ho Chi Minh, Vietnam. Peer reviewed |
 | Felice, F., LEY, C., Andreas Groll, & BORDAS, S. (2023). Statistically Enhanced Learning: a feature engineering framework to boost (any) learning algorithms. ORBilu-University of Luxembourg. https://orbilu.uni.lu/handle/10993/59205. |
 | DESHPANDE, S., LENGIEWICZ, J., & BORDAS, S. (27 June 2023). Novel Geometric Deep Learning Surrogate Framework for Non-Linear Finite Element Simulations [Poster presentation]. The Platform for Advanced Scientific Computing (PASC) Conference 2023. Peer reviewed |
 | Bulle, R., Barrera, O., BORDAS, S., Chouly, F., & HALE, J. (06 June 2023). An a posteriori error estimator for the spectral fractional power of the Laplacian [Paper presentation]. Large-Scale Scientific Computations, Sozopol, Bulgaria. |
 | LAVIGNE, T., BORDAS, S., & LENGIEWICZ, J. (March 2023). Identification of material parameters and traction field for soft bodies in contact. Computer Methods in Applied Mechanics and Engineering, 406, 115889. doi:10.1016/j.cma.2023.115889 Peer Reviewed verified by ORBi |
 | DESHPANDE, S., BORDAS, S., & LENGIEWICZ, J. (2023). MAgNET: A Graph U-Net Architecture for Mesh-Based Simulations. ORBilu-University of Luxembourg. https://orbilu.uni.lu/handle/10993/54969. doi:10.1016/j.engappai.2024.108055 |
 | DESHPANDE, S., SOSA, R. I., BORDAS, S., & LENGIEWICZ, J. (2023). Convolution, aggregation and attention based deep neural networks for accelerating simulations in mechanics. Frontiers in Materials. doi:10.3389/fmats.2023.1128954 Peer Reviewed verified by ORBi |
 | BULLE, R., HALE, J., Lozinski, A., BORDAS, S., & Chouly, F. (01 February 2023). Hierarchical a posteriori error estimation of Bank-Weiser type in the FEniCS Project. Computers and Mathematics with Applications, 131, 103-123. doi:10.1016/j.camwa.2022.11.009 Peer Reviewed verified by ORBi |
 | BULLE, R., Barrera, O., BORDAS, S., Chouly, F., & HALE, J. (2023). An a posteriori error estimator for the spectral fractional power of the Laplacian. Computer Methods in Applied Mechanics and Engineering, 407, 115943. doi:10.1016/j.cma.2023.115943 Peer Reviewed verified by ORBi |
 | RAJABI, M., LAVIGNE, T., SUAREZ AFANADOR, C. A., BORDAS, S., Sbalzarini, I. F., & OBEIDAT, A. (2023). Physics-informed Dynamic Graph Convolutional Neural Network with Curriculum Learning for Pore-scale Flow Simulations. Neural Networks. |
 | SUAREZ AFANADOR, C. A.* , Jakabčin, L., Lahellec, N., Maurel-Pantel, A., Boussaa, D., & BORDAS, S. (2023). Estimation des contraintes résiduelles dans des pièces composites imprimées 3D HT-FDM. Estimation of residual stresses in printed composite (SPC) parts [Paper presentation]. Journées Nationales sur les Composites, Besançon, France. Peer reviewed |
 | Jacquemin, T., SUCHDE, P., & BORDAS, S. (2023). Smart cloud collocation: geometry-aware adaptivity directly from CAD. Computer-Aided Design, 154, 103409. doi:10.1016/j.cad.2022.103409 Peer reviewed |
 | LAVIGNE, T., MAZIER, A., Perney, A., BORDAS, S., Hild, F., & LENGIEWICZ, J. (December 2022). Digital Volume Correlation for large deformations of soft tissues: Pipeline and proof of concept for the application to breast ex vivo deformations. Journal of the Mechanical Behavior of Biomedical Materials, 136, 105490. doi:10.1016/j.jmbbm.2022.105490 Peer Reviewed verified by ORBi |
 | SUAREZ AFANADOR, C. A., Cornaggia, R., Lahellec, N., Maurel-Pantel, A., Boussaa, D., Moulinec, H., & BORDAS, S. (November 2022). Effective thermo-viscoelastic behavior of short fiber reinforced thermo-rheologically simple polymers: An application to high temperature fiber reinforced additive manufacturing. European Journal of Mechanics. A, Solids, 96, 104701. doi:10.1016/j.euromechsol.2022.104701 Peer Reviewed verified by ORBi |
 | PAPAVASILEIOU, P., KORONAKI, E., POZZETTI, G., Kathrein, M., Czettl, C., Boudouvis, A. G., Mountziaris, T. J., & BORDAS, S. (October 2022). An efficient chemistry-enhanced CFD model for the investigation of the rate-limiting mechanisms in industrial Chemical Vapor Deposition reactors. Chemical Engineering Research and Design, 186, 314 - 325. doi:10.1016/j.cherd.2022.08.005 Peer Reviewed verified by ORBi |
 | DESHPANDE, S., LENGIEWICZ, J., & BORDAS, S. (01 August 2022). Probabilistic Deep Learning for Real-Time Large Deformation Simulations. Computer Methods in Applied Mechanics and Engineering, 398 (0045-7825), 115307. doi:10.1016/j.cma.2022.115307 Peer Reviewed verified by ORBi |
 | MAZIER, A., El Hadramy, S., Brunet, J.-N., HALE, J., Cotin, S., & BORDAS, S. (August 2022). SOniCS: Interfacing SOFA and FEniCS for advanced constitutive models [Paper presentation]. FEniCS 2022. |
 | DESHPANDE, S., LENGIEWICZ, J., & BORDAS, S. (2022). Real Time Hyper-elastic Simulations with Probabilistic Deep Learning. In 15th World Congress on Computational Mechanics (WCCM-XV). Peer reviewed |
 | MAZIER, A., LAVIGNE, T., LENGIEWICZ, J., DESHPANDE, S., URCUN, S., & BORDAS, S. (July 2022). Towards real-time patient-specific breast simulations: from full-field information to surrogate model [Paper presentation]. 9th World Congress of Biomechanics. |
 | URCUN, S., Lorenzo, G., Baroli, D., Rohan, P.-Y., Sciumè, G., Skalli, W., Lubrano, V., & BORDAS, S. (30 June 2022). Oncology and mechanics: landmark studies and promising clinical applications. Advances in Applied Mechanics, 55, 513-571. doi:10.1016/bs.aams.2022.05.003 Peer reviewed |
 | DESHPANDE, S., LENGIEWICZ, J., & BORDAS, S. (28 June 2022). Real-Time Large Deformation Simulations Using Probabilistic Deep Learning Framework [Poster presentation]. The Platform for Advanced Scientific Computing (PASC) Conference. |
 | FARINA, S., VOORSLUIJS, V., Claus, S., SKUPIN, A., & BORDAS, S. (07 June 2022). A CutFEM Method for a Mechanistic Modelling of Astrocytic Metabolism in 3D Physiological Morphologies [Paper presentation]. ECCOMAS Congress 2022, Oslo, Norway. |
ABBAD ANDALOUSSI, M., HUSCH, A., URCUN, S., & BORDAS, S. (06 June 2022). Imaging-informed BIOmechanical brain tumor forecast MOdelling [Paper presentation]. European Congres on COmputational Methods in Applied Sciences and engineering (ECCOMAS), Oslo, Norway. |
MONTORSI, C., FUSCO, A., VAN KERM, P., & BORDAS, S. (03 June 2022). Predicting depression in old age: Combining life course data with machine learning [Paper presentation]. Well-Being conference. |
 | DESHPANDE, S., LENGIEWICZ, J., & BORDAS, S. (2022). Real-time large deformations: A probabilistic deep learning approach. In The 8th European Congress on Computational Methods in Applied Sciences and Engineering. Peer reviewed |
 | JANSARI, C. V., Videla, J., Natarajan, S., BORDAS, S., & ATROSHCHENKO, E. (15 April 2022). Adaptive enriched geometry independent field approximation for 2D time-harmonic acoustics. Computers and Structures, 263, 106728. doi:10.1016/j.compstruc.2021.106728 Peer Reviewed verified by ORBi |
 | SUAREZ AFANADOR, C. A.* , Cornaggia, R., Maurel-Pantel, A., Lahellec, N., Boussa, D., Moulinec, H., Billon, N., BAROLI, D., & BORDAS, S. (2022). Mean-Field Approximations in Effective Thermo-viscoelastic Behavior for Composite Parts Obtained via Fused Deposition Modeling Technology. In T. E. Simos (Ed.), International Conference on Numerical Analysis and Applied Mathematics, ICNAAM 2020. American Institute of Physics Inc. doi:10.1063/5.0081430 Editorial reviewed |
 | Hauseux, P., Ambrosetti, A., BORDAS, S., & TKATCHENKO, A. (2022). Colossal Enhancement of Atomic Force Response in van der Waals Materials Arising from Many-Body Electronic Correlations. Physical Review Letters. doi:10.1103/PhysRevLett.128.106101 Peer Reviewed verified by ORBi |
 | MAZIER, A., Bilger, A., Forte, A. E., Peterlik, I., HALE, J., & BORDAS, S. (2022). Inverse deformation analysis: an experimental and numerical assessment using the FEniCS Project. Engineering with Computers. doi:10.1007/s00366-021-01597-z Peer Reviewed verified by ORBi |
 | FARINA, S., VOORSLUIJS, V., Fixemer, S., BOUVIER, D., Claus, S., BORDAS, S., & SKUPIN, A. (2022). 3D Modelling of a Spatially Resolved Energy Metabolism in Physiological Astrocytic Morphology [Paper presentation]. ECMTB 2022. |
 | LEIST, A., KLEE, M., KIM, J. H., Rehkopf, D., BORDAS, S., Muniz-Terrera, G., & Wade, S. (2022). Mapping of machine learning approaches for description, prediction, and causal inference in the social and health sciences. Science Advances, 8, 1942. doi:10.1126/sciadv.abk1942 Peer Reviewed verified by ORBi |
 | CHEN, L., Berke, P., Massart, T., BORDAS, S., & BEEX, L. (2022). An adaptive multiscale quasicontinuum approach for mechanical simulations of elastoplastic periodic lattices. Mechanics Research Communications, 126, 104019. doi:10.1016/j.mechrescom.2022.104019 Peer Reviewed verified by ORBi |
 | Bharadwaj, A. S., Kuhnert, J., BORDAS, S., & SUCHDE, P. (2022). A discrete droplet method for modelling thin film flows. Applied Mathematical Modelling, 112, 486--504. doi:10.1016/j.apm.2022.08.001 Peer Reviewed verified by ORBi |
 | URCUN, S., Rohan, P.-Y., Sciumè, G., & BORDAS, S. (30 November 2021). Cortex tissue relaxation and slow to medium load rates dependency can be captured by a two-phase flow poroelastic model. Journal of the Mechanical Behavior of Biomedical Materials, 126. doi:10.1016/j.jmbbm.2021.104952 Peer Reviewed verified by ORBi |
 | MAZIER, A., Ribes, S., Gilles, B., & BORDAS, S. (04 August 2021). A rigged model of the breast for preoperative surgical planning. Journal of Biomechanics, 128, 110645. doi:10.1016/j.jbiomech.2021.110645 Peer Reviewed verified by ORBi |
 | OBEIDAT, A., Andreas, T., BORDAS, S., & ZILIAN, A. (01 August 2021). Simulation of gas-dynamic, pressure surges and adiabatic compression phenomena in geometrically complex respirator oxygen valves. Thermal Science and Engineering Progress, 24. doi:10.1016/j.tsep.2021.100906 Peer reviewed |
 | ZERAATPISHEH, M., BEEX, L., & BORDAS, S. (2021). Bayesian model uncertainty quantification for hyperelastic soft tissue models. Data-Centric Engineering. doi:10.1017/dce.2021.9 Peer reviewed |
 | HALE, J., Schenone, E., BAROLI, D., BEEX, L., & BORDAS, S. (01 July 2021). A hyper-reduction method using adaptivity to cut the assembly costs of reduced order models. Computer Methods in Applied Mechanics and Engineering, 380, 113723. doi:10.1016/j.cma.2021.113723 Peer Reviewed verified by ORBi |
 | Spencer, R., Gkinis, P., KORONAKI, E., Gerogiorgis, D. I., BORDAS, S., & Boudouvis, A. G. (June 2021). Investigation of the chemical vapor deposition of Cu from copper amidinate through data driven efficient CFD modelling. Computers and Chemical Engineering, 149, 107289. doi:10.1016/j.compchemeng.2021.107289 Peer Reviewed verified by ORBi |
 | FARINA, S., Claus, S., HALE, J., VOORSLUIJS, V., SKUPIN, A., & BORDAS, S. (May 2021). Mechanistic modelling of astrocytic metabolism in physiological geometries reveals spatiotemporal effects potentially driving neurodegeneration [Paper presentation]. DTU DRIVEN Colloquium. |
 | Lee, C., Natarajan, S., HALE, J., Taylor, Z. A., Lee, J.-J., & BORDAS, S. (19 April 2021). Bubble-Enriched Smoothed Finite Element Methods for Nearly-Incompressible Solids. Computer Modeling in Engineering and Sciences, 127 (2), 411-436. doi:10.32604/cmes.2021.014947 Peer reviewed |
 | FARINA, S., Claus, S., HALE, J., SKUPIN, A., & BORDAS, S. (22 March 2021). A cut finite element method for spatially resolved energy metabolism models in complex neuro-cell morphologies with minimal remeshing. Advanced Modeling and Simulation in Engineering Sciences, 8, 5. doi:10.1186/s40323-021-00191-8 Peer Reviewed verified by ORBi |
 | LEIST, A., KLEE, M., KIM, J. H., Rehkopf, D., BORDAS, S., Muniz-Terrera, G., & Wade, S. (2021). Machine learning in the social and health sciences. ORBilu-University of Luxembourg. https://orbilu.uni.lu/handle/10993/47733. |
VIJAYARAGHAVAN, S., BEEX, L., BORDAS, S., & Noels, L. (January 2021). UNSUPERVISED LEARNING BASED MODEL ORDER REDUCTION FOR HYPERELASTOPLASTICITY [Paper presentation]. WCCM-ECCOMAS 2020. |
 | Piranda, B., Chodkiewicz, P., Holobut, P., BORDAS, S., Bourgeois, J., & LENGIEWICZ, J. (2021). Distributed Prediction of Unsafe Reconfiguration Scenarios of Modular Robotic Programmable Matter. IEEE Transactions on Robotics, 37 (6), 2226-2233. doi:10.1109/TRO.2021.3074085 Peer Reviewed verified by ORBi |
 | CHEN, L., BEEX, L., Berke, P., Massart, T., & BORDAS, S. (01 July 2020). Generalized quasicontinuum modeling of metallic lattices with geometrical and material nonlinearity and variability. Computer Methods in Applied Mechanics and Engineering, 366 (112878). doi:10.1016/j.cma.2020.112878 Peer reviewed |
 | MAZIER, A., Bilger, A., Forte, A., Peterlik, I., HALE, J., & BORDAS, S. (July 2020). Inverse simulation for retrieving the undeformed position for hyperelastic materials : application to breast simulations [Paper presentation]. WCCM 2020, Paris, France. |
 | DESHPANDE, S., BORDAS, S., BEEX, L., Cotin, S., & Sarkica, A. (July 2020). DATA DRIVEN SURGICAL SIMULATIONS [Paper presentation]. 14th World Congress on Computational Mechanics (WCCM), Paris, France. |
 | BULLE, R., BORDAS, S., Chouly, F., Lozinski, A., & HALE, J. (July 2020). Practical aspects of the Bank-Weiser estimator implementation and Biomechanics applications [Paper presentation]. 14th WCCM and ECCOMAS Congress, Paris, France. |
 | Al-Saad, M., SUAREZ AFANADOR, C. A., OBEIDAT, A., BORDAS, S., & Kulasegaram. (01 March 2020). Application of smooth particle hydrodynamics method for modelling blood flow with thrombus formation. Computer Modeling in Engineering and Sciences, 122 (3), 831-862. doi:10.32604/cmes.2020.08527 Peer reviewed |
 | Hu, Q., Xia, Y., Natarajan, S., ZILIAN, A., Hu, P., & BORDAS, S. (2020). Isogeometric analysis of thin Reissner-Mindlin shells: locking phenomena and B-bar method. Computational Mechanics, 65 (5), 1323-1341. doi:10.1007/s00466-020-01821-5 Peer Reviewed verified by ORBi |
 | Hołobut, P., LENGIEWICZ, J., & BORDAS, S. (2020). Autonomous model-based assessment of mechanical failures of reconfigurable modular robots with a Conjugate Gradient solver. In 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS) (pp. 11696-11702). IEEE. doi:10.1109/iros45743.2020.9341232 Peer reviewed |
 | Hauseux, P., Nguyen, T.-T., Ambrosetti, A., SALEME RUIZ, K., BORDAS, S., & TKATCHENKO, A. (2020). From quantum to continuum mechanics in the delamination of atomically-thin layers from substrates. Nature Communications. doi:10.1038/s41467-020-15480-w Peer Reviewed verified by ORBi |
 | BORDAS, S., PETERS, B., VITI, F., & ZILIAN, A. (2019). Data Centric Engineering and Data-Driven Modelling - Computational Engineering Lab Report 2019. (Report number 7 - 2019). Luxembourg, Luxembourg: UL. https://orbilu.uni.lu/handle/10993/42592 |
 | Elouneg, A., Sutula, D., SENSALE, M., Chouly, F., Chambert, J., Lejeune, A., BAROLI, D., HAUSEUX, P., BORDAS, S., & Jacquet, E. (09 December 2019). Mechanical parameters identification of keloid and surrounding healthy skin using Digital Image Correlation measurements in vivo [Paper presentation]. 24ème Congrès Français de Mécanique. |
 | Sutula, D., Elouneg, A., SENSALE, M., Chouly, F., Chambert, J., Lejeune, A., BAROLI, D., HAUSEUX, P., BORDAS, S., & Jacquet, E. (09 December 2019). Parameter identification problem in bimaterial human skin and sensitivity analysis : Uncertainties in biomechanics of skin [Paper presentation]. 24ème Congrès Français de Mécanique. |
 | MAZIER, A., DESHPANDE, S., & BORDAS, S. (November 2019). DIGITAL TWINNING FOR REAL-TIME SIMULATION [Poster presentation]. EIB Annual Economics Conference Tech Fair. |
 | Mohtarami, E., Baghbanan, A., Hashemolhosseini, H., & BORDAS, S. (13 September 2019). Fracture mechanism simulation of inhomogeneous anisotropic rocks by extended finite element method. Theoretical and Applied Fracture Mechanics, 104. doi:10.1016/j.tafmec.2019.102359 Peer Reviewed verified by ORBi |
CHEN, L., Berke, P., BEEX, L., Massart, T., & BORDAS, S. (12 September 2019). Adaptive equation-free multiscale modeling of metallic lattices with geometrical nonlinearity and variability [Paper presentation]. 2nd International Conference on Simulation for Additive Manufacturing, Pavia, Italy. |
CHEN, L., Berke, P., BEEX, L., Massart, T., & BORDAS, S. (05 September 2019). Equation-free multiscale modeling of metallic lattices with geometrical and material nonlinearity and variability [Paper presentation]. 15th International Conference on Computational Plasticity, Barcelona, Spain. |
 | JACQUEMIN, T. A. M., TOMAR, S., AGATHOS, K., Mohseni-Mofidi, S., & BORDAS, S. (2019). Taylor-Series Expansion Based Numerical Methods: A Primer, Performance Benchmarking and New Approaches for Problems with Non-smooth Solutions. Archives of Computational Methods in Engineering. doi:10.1007/s11831-019-09357-5 Peer reviewed |
 | OBEIDAT, A., & BORDAS, S. (15 August 2019). An Implicit boundary approach for viscous compressible high Reynolds flows using hybrid remeshed particle hydrodynamics method. Journal of Computational Physics, 391, 347-364. doi:10.1016/j.jcp.2019.01.041 Peer Reviewed verified by ORBi |
 | VIJAYARAGHAVAN, S., BEEX, L., Noels, L., & BORDAS, S. (29 July 2019). Clustering Based Model Order Reduction For Hyper Elastoplastic Material Models [Paper presentation]. US National Congress on Computational Mechanics. |
 | Mathew, T., BEEX, L., BORDAS, S., & Natarajan, S. (July 2019). A stochastic Galerkin cell-based smoothed finite element method (SGCS-FEM). International Journal of Computational Methods, 17 (8). doi:10.1142/S0219876219500543 Peer Reviewed verified by ORBi |
 | Cascio, M., BAROLI, D., BORDAS, S., Deretzis, I., Falci, G., Magliano, A., & La Magna, A. (17 June 2019). Coupled molecular-dynamics and finite-element-method simulations for the kinetics of particles subjected to field-mediated forces. Physical Review. E, Statistical, Nonlinear, and Soft Matter Physics, 99 (6). doi:10.1103/PhysRevE.99.063307 Peer Reviewed verified by ORBi |
 | Chen, L. L., LIAN, H., Chen, H. B., Atroshchenko, E., & BORDAS, S. (12 June 2019). Structural shape optimization of three dimensional acoustic problems with isogeometric boundary element methods. Computer Methods in Applied Mechanics and Engineering, 355, 926-951. doi:10.1016/j.cma.2019.06.012 Peer Reviewed verified by ORBi |
 | Kosec, G., Slak, J., Depolli, M., Trobec, R., Pereira, K., TOMAR, S., JACQUEMIN, T. A. M., BORDAS, S., & Wahab, M. A. (28 May 2019). Weak and strong from meshless methods for linear elastic problem under fretting contact conditions. Tribology International, 138, 392-402. doi:10.1016/j.triboint.2019.05.041 Peer Reviewed verified by ORBi |
 | BORDAS, S., BEEX, L., CHEN, L., VIJAYARAGHAVAN, S., Kerfriden, P., Goury, O., Massart, T., & Noels, L. (13 May 2019). Multiscale fracture: a natural connection between reduced order models and homogenisation [Paper presentation].
First Benelux Workshop on damage and fracture ESIS2019, Antwerp, Belgium. |
 | BORDAS, S., & Natarajan, S. (03 May 2019). Displacement based polytopal elements a strain smoothing and scaled boundary approach [Paper presentation]. POEMS2019, Marseille, France. |
 | Anitescu, C., Atroshchenko, E., BORDAS, S., DING, C., Jansari, C., LIAN, H., Natarajan, S., SUAREZ AFANADOR, C. A., TOMAR, S., & Videla, J. (11 April 2019). ADVANCES IN GEOMETRY INDEPENDENT APPROXIMATIONS [Paper presentation]. SYMCOMP 2019, Portugal. |
 | Feng, S. Z., BORDAS, S., Han, X., Wang, G., & Li, Z. X. (22 March 2019). A gradient weighted extended finite element method (GW-XFEM) for fracture mechanics. Acta Mechanica, 230, 2385–2398. doi:10.1007/s00707-019-02386-y Peer Reviewed verified by ORBi |
 | Katili, I., Maknun, I. J., Katili, A. M., BORDAS, S., & Natarajan, S. (06 March 2019). A unified polygonal locking-free thin/thick smoothed plate element. Composite Structures, 219, 147-157. doi:10.1016/j.compstruct.2019.03.020 Peer Reviewed verified by ORBi |
 | BORDAS, S., LIAN, H., & DING, C. (2019). Introduction to Isogeometric Analysis. https://orbilu.uni.lu/handle/10993/38749 |
 | Agathos, K., Chatzi, E., & BORDAS, S. (07 February 2019). A unified enrichment approach addressing blending and conditioning issues in enriched finite elements. Computer Methods in Applied Mechanics and Engineering, 349, 673-700. doi:10.1016/j.cma.2019.02.005 Peer Reviewed verified by ORBi |
 | DING, C., Deokar, R. R., Ding, Y., Li, G., Cui, X., Tamma, K. K., & BORDAS, S. (03 February 2019). Model order reduction accelerated Monte Carlo stochastic isogeometric method for the analysis of structures with high-dimensional and independent material uncertainties. Computer Methods in Applied Mechanics and Engineering, 349, 266-284. doi:10.1016/j.cma.2019.02.004 Peer Reviewed verified by ORBi |
 | Bansal, M., Singh, I. V., Patil, R. U., Claus, S., & BORDAS, S. (01 February 2019). A simple and robust computational homogenization approach for heterogeneous particulate composites. Computer Methods in Applied Mechanics and Engineering, 349, 45-90. doi:10.1016/j.cma.2019.02.001 Peer Reviewed verified by ORBi |
 | BORDAS, S. (2019). Modelling Complex Systems: a primer - agent-based models, equation-based models, statistical models and Bayesian inference, digital twins. (Continuing Education, University of Luxembourg). |
 | Khajah, T., Antoine, X., & BORDAS, S. (21 January 2019). B-Spline FEM for Time-Harmonic Acoustic Scattering and Propagation. Journal of Theoretical and Computational Acoustics, 27. doi:10.1142/S2591728518500597 Peer reviewed |
 | Francis, A., Natarajan, S., Atroshchenko, E., Lévy, B., & BORDAS, S. (09 January 2019). A one point integration rule over star convex polytopes. Computers and Structures, 215, 43-64. doi:10.1016/j.compstruc.2019.01.001 Peer Reviewed verified by ORBi |
 | Yang, J., LIAN, H., Liang, W., Nguyen, V. P., & BORDAS, S. (06 January 2019). Model I cohesive zone models of different rank coals. International Journal of Rock Mechanics and Mining Sciences, 115, 145-156. doi:10.1016/j.ijrmms.2019.01.001 Peer Reviewed verified by ORBi |
 | BORDAS, S. (04 January 2019). Meshing or not meshing - Iso/sub/super-geometric analysis (adaptive unfitted methods for real-time simulations) Immersed collocation methods
[Paper presentation]. UCL Workshop on unfitted methods, London, United Kingdom. |
 | RAPPEL, H., BEEX, L., Noels, L., & BORDAS, S. (January 2019). Identifying elastoplastic parameters with Bayes' theorem considering double error sources and model uncertainty. Probabilistic Engineering Mechanics, 55, 28-41. doi:10.1016/j.probengmech.2018.08.004 Peer Reviewed verified by ORBi |
 | RAPPEL, H., BEEX, L., HALE, J., Noels, L., & BORDAS, S. (2019). A Tutorial on Bayesian Inference to Identify Material Parameters in Solid Mechanics. Archives of Computational Methods in Engineering, 1-25. doi:10.1007/s11831-018-09311-x Peer reviewed |
 | Barbosa, J., BORDAS, S., Carvalho, A., DING, C., LIAN, H., Loja, M. A., Mathew, T., Natarajan, S., RAPPEL, H., Rodrigues, J., & SUAREZ AFANADOR, C. A. (2019). Geometrical and material uncertainties for the mechanics of composites [Paper presentation]. IGA 2019. |
 | Videla, J., Anitescu, C., Khajah, T., BORDAS, S., & Atroshchenko, E. (16 December 2018). h- and p-adaptivity driven by recovery and residual-based error estimators for PHT-splines applied to time-harmonic acoustics. Computers and Mathematics with Applications, 77 (9), 2369-2395. doi:10.1016/j.camwa.2018.12.026 Peer Reviewed verified by ORBi |
 | Chen, Y., LIAN, H., Liang, W., Yang, J., Nguyen, V. P., & BORDAS, S. (21 November 2018). The influence of fracture geometry variation on non-Darcy flow in fractures under confining stresses. International Journal of Rock Mechanics and Mining Sciences, 113, 59-71. doi:10.1016/j.ijrmms.2018.11.017 Peer Reviewed verified by ORBi |
 | Surendran, M., Natarajan, S., Palani, G. S., & BORDAS, S. (02 November 2018). Linear smoothed extended finite element method for fatigue crack growth simulations. Engineering Fracture Mechanics, 206, 551-564. doi:10.1016/j.engfracmech.2018.11.011 Peer Reviewed verified by ORBi |
 | Ortiz-Bernardin, A., Köbrich, P., HALE, J., Olate-Sanzana, E., BORDAS, S., & Natarajan, S. (01 November 2018). A volume-averaged nodal projection method for the Reissner-Mindlin plate model. Computer Methods in Applied Mechanics and Engineering, 341, 827-850. doi:10.1016/j.cma.2018.07.023 Peer reviewed |
 | HALE, J., Brunetti, M., BORDAS, S., & Maurini, C. (15 October 2018). Simple and extensible plate and shell finite element models through automatic code generation tools. Computers and Structures, 209, 163-181. doi:10.1016/j.compstruc.2018.08.001 Peer Reviewed verified by ORBi |
 | BUI, H. P., TOMAR, S., & BORDAS, S. (12 October 2018). Corotational cut finite element method for real-time surgical simulation: Application to needle insertion simulation. Computer Methods in Applied Mechanics and Engineering, 345, 183-211. doi:10.1016/j.cma.2018.10.023 Peer Reviewed verified by ORBi |
 | Lin, X., Zhu, H., Yuan, X., Wang, Z., & BORDAS, S. (October 2018). The elastic properties of composites reinforced by a transversely isotropic random fibre-network. Composite Structures, 208, 33-44. doi:10.1016/j.compstruct.2018.09.097 Peer Reviewed verified by ORBi |
 | BORDAS, S. (2018). Lack of separation of scales: A view from reduced order modelling and homogenisation
[Paper presentation]. SAFEFLY - Summer School, Nottingham, United Kingdom. |
 | Koronaki, E. D., Gkinis, P. A., BEEX, L., BORDAS, S., & Theodoropoulos, C. (September 2018). Classification of states and model order reduction of large scale Chemical Vapor Deposition processes with solution multiplicity. Computers and Chemical Engineering, 121, 148-157. doi:10.1016/j.compchemeng.2018.08.023 Peer Reviewed verified by ORBi |
 | Agathos, K., BORDAS, S., & Chatzi, E. (2018). Improving the conditioning of XFEM/GFEM for fracture mechanics problems through enrichment quasi-orthogonalization. Computer Methods in Applied Mechanics and Engineering. doi:10.1016/j.cma.2018.08.007 Peer reviewed |
 | HAUSEUX, P., HALE, J., BULLE, R., Chouly, F., Lozinski, A., & BORDAS, S. (23 July 2018). Uncertainty Quantification in Finite Element Models:Application to SoftTissue Biomechanics [Paper presentation]. 13th World Congress in Computational Mechanics (WCCM XIII). |
 | RAPPEL, H., BEEX, L., & BORDAS, S. (23 July 2018). Identifying fibre material parameter distributions with little experimental efforts [Paper presentation]. 13th World Congress in Computational Mechanics. |
 | RAPPEL, H., BEEX, L., & BORDAS, S. (22 July 2018). Identifying material parameter distributions of fibers with extremely limited experimental efforts [Paper presentation]. 13th World Congress in Computational Mechanics. |
BORDAS, S. (05 March 2018). Free boundary problems: numerical methods and data-driven simulations [Paper presentation]. Oxford Engineering Mechanics Seminar, Oxford, United Kingdom. |
 | BORDAS, S. (08 February 2018). Data-driven modelling and simulation: fracture and medical simulations [Paper presentation]. Jožef Stefan Institute Seminar Series, Ljubljana, Slovenia. |
 | Agathos, K., Chatzi, E., & BORDAS, S. (2018). Multiple crack detection in 3D using a stable XFEM and global optimization. Computational Mechanics. doi:10.1007/s00466-017-1532-y Peer Reviewed verified by ORBi |
 | Akbari, A., Kerfriden, P., & BORDAS, S. (February 2018). On the effect of grains interface parameters on the macroscopic properties of polycrystalline materials. Computers and Structures, 196, 355-368. doi:10.1016/j.compstruc.2017.09.005 Peer Reviewed verified by ORBi |
 | HALE, J., HAUSEUX, P., & BORDAS, S. (08 January 2018). Using higher-order adjoints to accelerate the solution of UQ problems with random fields [Poster presentation]. Key UQ methodologies and motivating applications, Cambridge, United Kingdom. |
 | Nguyen, T., Kashani, A., Ngo, T., & BORDAS, S. (2018). Deep neural network with high-order neuron for the prediction of foamed concrete strength. Computer-Aided Civil and Infrastructure Engineering. doi:10.1111/mice.12422 Peer Reviewed verified by ORBi |
 | Hu, Q., Chouly, F., Hu, P., Cheng, G., & BORDAS, S. (2018). Skew-symmetric Nitsche’s formulation in isogeometric analysis: Dirichlet and symmetry conditions, patch coupling and frictionless contact. Computer Methods in Applied Mechanics and Engineering, 341, 188-220. doi:10.1016/j.cma.2018.05.024 Peer reviewed |
 | BORDAS, S., & ZILIAN, A. (2018). 2018 Lab Report Computational Mechanics Legato-team and Z-team. (2018). University of Luxembourg. https://orbilu.uni.lu/handle/10993/33806 |
 | BEEX, L., BORDAS, S., HALE, J., PETERS, B., & ZILIAN, A. (2018). ECCOMAS Newsletter - Computational and Data Sciences in Luxembourg. https://orbilu.uni.lu/handle/10993/36574 |
 | Bansal, M., Singh, I. V., Mishra, B. K., & BORDAS, S. (2018). A parallel and efficient multi-split XFEM for 3-D analysis of heterogeneous materials. Computer Methods in Applied Mechanics and Engineering. doi:10.1016/j.cma.2018.12.023 Peer reviewed |
 | Atroshchenko, E., TOMAR, S., Xu, G., & BORDAS, S. (2018). Weakening the tight coupling between geometry and simulation in isogeometric analysis: from sub- and super- geometric analysis to Geometry Independent Field approximaTion (GIFT). International Journal for Numerical Methods in Engineering. doi:10.1002/nme.5778 Peer Reviewed verified by ORBi |
 | HAUSEUX, P., HALE, J., Cotin, S., & BORDAS, S. (2018). Quantifying the uncertainty in a hyperelastic soft tissue model with stochastic parameters. Applied Mathematical Modelling, 62, 86-102. doi:10.1016/j.apm.2018.04.021 Peer Reviewed verified by ORBi |
 | NGUYEN, T. T., Réthoré, J., Bolivar, J., Baietto, M.-C., Fregonese, M., & BORDAS, S. (2018). Modelling of inter- and transgranular stress corrosion crack propagation in polycrystalline material by using phase field method. Journal of the Mechanical Behavior of Materials, 26, 181--191. Peer reviewed |
 | Nguyen, T., Ghazlan, A., Kashani, A., BORDAS, S., & Ngo, T. (2018). 3D meso-scale modelling of foamed concrete based on X-ray Computed Tomography. Construction and Building Materials, 188, 583-598. doi:10.1016/j.conbuildmat.2018.08.085 Peer reviewed |
 | HAUSEUX, P., & BORDAS, S. (2018). Final Report IRP MOmENTUM Needle insertion simulation. UL. https://orbilu.uni.lu/handle/10993/36295 |
 | Yu, P., Anitescu, C., TOMAR, S., BORDAS, S., & Kerfriden, P. (2018). Adaptive Isogeometric analysis for plate vibrations: An efficient approach of local refinement based on hierarchical a posteriori error estimation. Computer Methods in Applied Mechanics and Engineering, 342, 251-286. doi:10.1016/j.cma.2018.08.010 Peer reviewed |
 | Xu, G., Li, M., Mourrain, B., Rabczuk, T., Xu, J., & BORDAS, S. (2018). Constructing IGA-suitable planar parameterization from complex CAD boundary by domain partition and global/local optimization. Computer Methods in Applied Mechanics and Engineering, 328, 175-200. doi:10.1016/j.cma.2017.08.052 Peer reviewed |
 | BORDAS, S. (20 December 2017). Computational Sciences and the Transition to Data-Driven Modelling and Simulation: Case studies in Engineering & Personalised Medicine - Presentation for the 50 years of Inria and the 10 years of ERC [Paper presentation]. 50 years of Inria (and 10 years of ERC), Grand Est, Nancy, France, Nancy, France. |
 | HAUSEUX, P., HALE, J., & BORDAS, S. (20 December 2017). Calculating the Malliavin derivative of some stochastic mechanics problems. PLoS ONE, 12 (12), 0189994. doi:10.1371/journal.pone.0189994 Peer Reviewed verified by ORBi |
 | Atroshchenko, E., HALE, J., Videla, J. A., Potapenko, S., & BORDAS, S. (October 2017). Micro-structured materials: inhomogeneities and imperfect interfaces in plane micropolar elasticity, a boundary element approach. Engineering Analysis with Boundary Elements, 83, 195-203. doi:10.1016/j.enganabound.2017.07.023 Peer Reviewed verified by ORBi |
 | HAUSEUX, P., HALE, J., & BORDAS, S. (September 2017). Uncertainty Quantification (Monte Carlo methods) - Sensitivity Analysis - Biomechanics [Paper presentation]. Legato Team seminar. |
 | HU, Q., Xia, Y., Natarajan, S., ZILIAN, A., Hu, P., & BORDAS, S. (2017). Isogeometric analysis of thin Reissner-Mindlin plates and shells: Locking phenomena and generalized local B-bar method. ORBilu-University of Luxembourg. https://orbilu.uni.lu/handle/10993/32445. |
 | RAPPEL, H., BEEX, L., & BORDAS, S. (2017). Bayesian inference to identify parameters in viscoelasticity. Mechanics of Time-Dependent Materials. doi:10.1007/s11043-017-9361-0 Peer reviewed |
 | BORDAS, S. (2017). Discretisation and Model Selection for Interface Problems in Mechanics. International Journal of Computational Methods. Peer Reviewed verified by ORBi |
 | SENSALE, M., Chambert, J., Chouly, F., Arnaud, L., S., J., K., R., G., R., T., L., B., C., Patrick, S., Emmanuelle, J., & BORDAS, S. (August 2017). Experimental and numerical assessment of the mechanics of keloid-skin composites undergoing large deformations [Paper presentation]. EUROMECH Colloquim 595, Lille, France. |
 | BUI, H. P., TOMAR, S., Courtecuisse, H., Cotin, S., & BORDAS, S. (August 2017). Real-time Error Control for Surgical Simulation: Application to Percutaneous Interventions [Paper presentation]. Euromech 595, Lille, France. |
 | BORDAS, S. (12 July 2017). Error-controlled computational fracture mechanics [Paper presentation]. DAMAS12th International Conference on Damage Assessment of Structures 2017, Kitakyushu, Japan, 10-12 July 2017 http://www.damas.ugent.be/, Kitakyushu, Japan. |
 | BORDAS, S. (21 June 2017). Advances in enriched finite element formulations for fracture and cutting: engineering and surgical simulation applications [Paper presentation]. XDMS2017 Plenary Lecture at eXtended Discretization methodS for PDEs on complex and evolving domains, Umeå, Sweden. |
BORDAS, S. (2017). Towards a seamless Integration of CAD and Simulation: CISM Course 2017. (2017, International Centre for Mechanical Sciences - Centre International des Sciences Mécaniques, Udine, Italy, courses_C1704_C1704_Beer_Bordas). Udine, Italy: CISM. |
 | OBEIDAT, A., & BORDAS, S. (2017). Three-dimensional remeshed smoothed particle hydrodynamics for the simulation of isotropic turbulence. International Journal for Numerical Methods in Fluids. doi:10.1002/fld.4405 Peer Reviewed verified by ORBi |
 | Khajah, T., Antoine, X., & BORDAS, S. (15 May 2017). High Frequency Acoustic Scattering in Isogeometric Analysis [Paper presentation]. WAVES 2017, University of Minnesota, United States. |
 | HAUSEUX, P., HALE, J., & BORDAS, S. (01 May 2017). Accelerating Monte Carlo estimation with derivatives of high-level finite element models. Computer Methods in Applied Mechanics and Engineering, 318, 917-936. doi:10.1016/j.cma.2017.01.041 Peer reviewed |
 | Nguyen, V. P., Lian, H., Rabczuk, T., & BORDAS, S. (20 April 2017). Modelling hydraulic fractures in porous media using flow cohesive interface elements. Engineering Geology, 225, 68-82. doi:10.1016/j.enggeo.2017.04.010 Peer Reviewed verified by ORBi |
 | Lee, C.-K., Mihai, L. A., HALE, J., Kerfriden, P., & BORDAS, S. (01 April 2017). Strain smoothed for compressible and nearly-incompressible finite elasticity. Computers and Structures, 182, 540-555. doi:10.1016/j.compstruc.2016.05.004 Peer Reviewed verified by ORBi |
 | Ley, C., & BORDAS, S. (2017). What makes Data Science different? A discussion involving Statistics2.0 and Computational Sciences. ORBilu-University of Luxembourg. https://orbilu.uni.lu/handle/10993/30235. |
 | BAROLI, D., BEEX, L., HALE, J., & BORDAS, S. (10 March 2017). Reduced basis Nitsche-based domain decomposition: a biomedical application [Paper presentation]. Applications of Model Order Reduction Methods in Industrial Research and Development. |
 | BUI, H. P., TOMAR, S., & BORDAS, S. (2017). Real-time Error Control for Surgical Simulation. ORBilu-University of Luxembourg. https://orbilu.uni.lu/handle/10993/29846. |
 | HAUSEUX, P., HALE, J., & BORDAS, S. (February 2017). Uncertainty Quantification - Sensitivity Analysis / Biomechanics [Paper presentation]. Groupe de Travail, Besançon, France. |
 | PALMIROTTA, G., BORDAS, S., & Melakessou, F. (2017). 3D-Foot Plantar Pressure Reconstruction based on the IEE Foot Smart Insole. ORBilu-University of Luxembourg. https://orbilu.uni.lu/handle/10993/49867. |
 | Martínez-Pañeda, E., Natarajan, S., & BORDAS, S. (2017). Gradient plasticity crack tip characterization by means of the extended finite element method. Computational Mechanics. doi:10.1007/s00466-017-1375-6 Peer Reviewed verified by ORBi |
 | AGATHOS, K., Ventura, G., Chatzi, E., & BORDAS, S. (2017). Stable 3D XFEM/vector-level sets for non-planar 3D crack propagation and comparison of enrichment schemes. International Journal for Numerical Methods in Engineering. doi:10.1002/nme.5611 Peer Reviewed verified by ORBi |
 | Paladim, D.-A., de Almeida, J. P. B., BORDAS, S., & Kerfriden, P. (2017). Guaranteed error bounds in homogenisation: an optimum stochastic approach to preserve the numerical separation of scales. International Journal for Numerical Methods in Engineering, 110 (2), 103–132. doi:10.1002/nme.5348 Peer Reviewed verified by ORBi |
 | Wan, D., Hu, D., Natarajan, S., BORDAS, S., & Long, T. (2017). A linear smoothed quadratic finite element for the analysis of laminated composite Reissner–Mindlin plates. Composite Structures, 180, 395-411. doi:10.1016/j.compstruct.2017.07.092 Peer reviewed |
 | Wan, D., Hu, D., Natarajan, S., BORDAS, S., & Yang, G. (2017). A fully smoothed XFEM for analysis of axisymmetric problems with weak discontinuities. International Journal for Numerical Methods in Engineering, 110 (3), 203-226. doi:10.1002/nme.5352 Peer reviewed |
 | Wan, D., Hu, D., Natarajan, S., BORDAS, S., & Long, T. (2017). A linear smoothed higher-order CS-FEM for the analysis of notched laminated composites. Engineering Analysis with Boundary Elements, 85, 127-135. doi:10.1016/j.enganabound.2017.10.003 Peer Reviewed verified by ORBi |
 | Deng, J., Zhou, G., BORDAS, S., Xiang, C., & Cai, D. A. (2017). Numerical evaluation of buckling behaviour induced by compression on patch-repaired composites. Composite Structures, 168, 582-596. doi:10.1016/j.compstruct.2016.12.071 Peer reviewed |
 | Phuoc Bui, H., Tomar, S., Courtecuisse, H., Cotin, S., & BORDAS, S. (2017). Real-time Error Control for Surgical Simulation. IEEE Transactions on Biomedical Engineering. doi:10.1109/TBME.2017.2695587 Peer Reviewed verified by ORBi |
 | Hirshikesh, Natarajan, S., Ratna Kumar, A. K., BORDAS, S., & Atroshchenko, E. (2017). Trefftz polygonal finite element for linear elasticity: convergence, accuracy, and properties. Asia Pacific Journal on Computational Engineering. doi:10.1186/s40540-017-0020-3 Peer Reviewed verified by ORBi |
 | Sinaie, S., NGUYEN, V. H., Nguyen, C. T., & BORDAS, S. (2017). Programming the material point method in Julia. Advances in Engineering Software, 105, 17-29. doi:10.1016/j.advengsoft.2017.01.008 Peer reviewed |
 | BOURANTAS, G., Loukopoulos, V. C., Chowdhury, H. A., Joldes, G. R., MILLER, K., & BORDAS, S. (2017). An implicit potential method along with a meshless technique for incompressible fluid flows for regular and irregular geometries in 2D and 3D. Engineering Analysis with Boundary Elements, 77, 97-111. doi:10.1016/j.enganabound.2017.01.009 Peer reviewed |
 | Jin, Y., González-Estrada, O. A., Pierard, O., & BORDAS, S. (2017). Error-controlled adaptive extended finite element method for 3D linear elastic crack propagation. Computer Methods in Applied Mechanics and Engineering, 318, 319-348. doi:10.1016/j.cma.2016.12.016 Peer reviewed |
 | BORDAS, S. (2016). Computational Sciences Year 2016 Activity Report. (1). UL. https://orbilu.uni.lu/handle/10993/33817 |
 | BUI, H. P., TOMAR, S., Courtecuisse, H., Cotin, S., & BORDAS, S. (12 December 2016). Real-time error control for surgical simulation [Poster presentation]. Computational Sciences for Medicine, Luxembourg, Luxembourg. |
 | RAPPEL, H., BEEX, L., HALE, J., & BORDAS, S. (12 December 2016). Bayesian inference for parameter identification in computational mechanics [Poster presentation]. Computational Sciences for Medicine Workshop, Luxembourg, Luxembourg. |
 | HALE, J., Farrell, P., & BORDAS, S. (12 December 2016). Elastography under uncertainty [Poster presentation]. Computational Sciences for Medicine Modelling and Simulation for Surgery, Luxembourg, Luxembourg. |
 | BAROLI, D., HAUSEUX, P., HALE, J., & BORDAS, S. (12 December 2016). Image to analysis pipeline: single and double balloons kyphoplasty [Poster presentation]. Residential Workshop on Computational Sciences for Medical Simulation. |
 | SUTULA, D., AGATHOS, K., ZIAEI RAD, V., Francis, A., Natarajan, S., HALE, J., & BORDAS, S. (December 2016). Numerical methods for fracture/cutting of heterogeneous materials [Paper presentation]. Computational Sciences for Medicine Workshop 2016 Dec 12-14 Luxembourg, Luxembourg. |
 | HAUSEUX, P., HALE, J., & BORDAS, S. (December 2016). Uncertainty quantification for soft tissue biomechanics [Poster presentation]. Computational Sciences for Medicine Workshop 2016 Dec 12-14 Luxembourg. |
 | Lian, H., Pierre, K., & BORDAS, S. (2016). Shape Optimization Directly from CAD: an Isogeometric Boundary Element Approach Using T-splines. University of Luxembourg. https://orbilu.uni.lu/handle/10993/17838 |
 | Khajah, T., Antoine, X., & BORDAS, S. (2016). Isogeometric finite element analysis of time-harmonic exterior acoustic scattering problems. ORBilu-University of Luxembourg. https://orbilu.uni.lu/handle/10993/28645. |
 | RAPPEL, H., BEEX, L., HALE, J., & BORDAS, S. (07 September 2016). Bayesian inference for material parameter identification in elastoplasticity [Paper presentation]. European Mechanics of Materials Conference (EMMC15), Brussels, Belgium. |
 | HAUSEUX, P., HALE, J., & BORDAS, S. (September 2016). Stochastic FE analysis of brain deformation with different hyper-elastic models [Paper presentation]. Computer Methods in Biomechanics and Biomedical Engineering, Tel Aviv, Israel. |
 | BORDAS, S., Kerfriden, P., Beex, L., Goury, O., Akbari, A., Hale, J., Hauseux, P., & Rappel, H. (2016). Multi-scale modelling of fracture [Paper presentation]. Texas A&M Mechanical Engineering Seminar, College Station, Texas, United States. |
 | Loukopoulos, V., BOURANTAS, G., Lampropoulos, D., Nikiforidis, V.-M., BORDAS, S., & Nikiforidis, G. (15 July 2016). Numerical studies of magnetic particles concentration in biofluid (blood) under the influence of high gradient magnetic field in microchannel [Paper presentation]. ECCOMAS 2016. |
 | Peng, X., Atroshchenko, E., Kerfriden, P., & BORDAS, S. (2016). Linear elastic fracture simulation directly from CAD: 2D NURBS-based implementation and role of tip enrichment. International Journal of Fracture. doi:10.1007/s10704-016-0153-3 Peer Reviewed verified by ORBi |
 | BORDAS, S., Kerfriden, P., Courtecuisse, H., Duriez, C., Cotin, S., Goury, O., TOMAR, S., Huu Bui, P., Hauseux, P., & Hale, J. (2016). Simulating topological changes in real time for surgical assistance [Paper presentation]. Hamlyn Symposium, London, United Kingdom. |
 | RAPPEL, H., BEEX, L., HALE, J., & BORDAS, S. (09 June 2016). A Bayesian approach for parameter identification in elastoplasticity [Paper presentation]. ECCOMAS Congress 2016, Crete Island, Greece. |
 | ZIAEI RAD, V., HALE, J., Maurini, C., & BORDAS, S. (08 June 2016). Phase field approach to fracture: Towards the simulation of cutting soft tissues [Paper presentation]. European Congress on Computational Methods in Applied Sciences and Engineering. |
 | TOMAR, S., Atroshchenko, E., Xu, G., & BORDAS, S. (07 June 2016). Weakening the tight coupling between geometry and simulation in isogeometric analysis [Paper presentation]. 7th European Congress on Computational Methods in Applied Sciences and Engineering 2016, Crete, Greece. |
 | BORDAS, S., TOMAR, S., Atroshchenko, E., & Xu, G. (05 June 2016). Weakening the tight coupling between geometry and simulation in isogeometric analysis [Paper presentation]. ECCOMAS Congress 2016, Crete Island, Greece. |
 | TOMAR, S., Atroshchenko, E., Xu, G., & BORDAS, S. (02 June 2016). Generalizing the isogeometric concept: weakening the tight coupling between geometry and simulation in IGA [Paper presentation]. High-Order Finite Element and Isogeometric Methods 2016, Jerusalem, Israel. |
 | Natarajan, S., TOMAR, S., BORDAS, S., Francis, A., & Ortiz-Bernardin, A. (June 2016). Linear smoothing over arbitrary polytopes for compressible and nearly incompressible linear elasticity [Paper presentation]. ECCOMAS 2016, Crete Island, Greece. |
 | RAPPEL, H., BEEX, L., HALE, J., & BORDAS, S. (June 2016). A Bayesian approach for parameter identification in elastoplasticity [Paper presentation]. ECCOMAS Congress 2016, Crete Island, Greece. |
 | Loukopoulos, V., BOURANTAS, G., Labropoulos, D., Nikiforidis, V.-M., BORDAS, S., & Nikiforidis, G. (June 2016). Numerical study of magnetic particles concentration in biofluid (blood) under the influence of high gradient magnetic field in microchannel [Paper presentation]. ECCOMAS 2016. |
 | AGATHOS, K., Ventura, G., Chatzi, E., & BORDAS, S. (June 2016). Well Conditioned and Optimally Convergent Extended Finite Elements and Vector Level Sets for Three-Dimensional Crack Propagation [Paper presentation]. ECCOMAS Congress 2016, Crete Island, Greece. |
 | BEEX, L., & BORDAS, S. (June 2016). Virtual-power-based quasicontinuum methods for discrete dissipative materials [Paper presentation]. 7th European Congress on Computational Methods in Applied Sciences and Engineering, Crete Island, Greece. |
HAUSEUX, P., HALE, J., & BORDAS, S. (June 2016). Efficient propagation of uncertainty through an inverse non-linear deformation model of soft tissue [Paper presentation]. European Congress on Computational Methods in Applied Sciences and Engineering. |
 | Peng, X., Atroshchenko, E., Kerfriden, P., & BORDAS, S. (2016). Isogeometric boundary element methods for three dimensional static fracture and fatigue crack growth. Computer Methods in Applied Mechanics and Engineering. doi:10.1016/j.cma.2016.05.038 Peer reviewed |
BORDAS, S., TOMAR, S., Atroshchenko, E., & Xu, G. (30 May 2016). Generalizing the isogeometric concept: weakening the tight coupling between geometry and simulation in IGA [Paper presentation]. HOFEIM 2016, Jerusalem, Israel. |
 | BORDAS, S. (22 May 2016). Computational mechanics of interfaces [Paper presentation]. GIAN Course in Multiscale Analysis, Madras/Chennai, India. |
 | RAPPEL, H., BEEX, L., HALE, J., & BORDAS, S. (2016). Bayesian inference for material parameter identification. Luxembourg, Luxembourg: University of Luxembourg. https://orbilu.uni.lu/handle/10993/27346 |
 | HAUSEUX, P., HALE, J., & BORDAS, S. (09 May 2016). Propagating uncertainty using FE advanced Monte-Carlo methods: application to non- linear hyperelastic models [Paper presentation]. internal report. |
 | BAROLI, D., BEEX, L., & BORDAS, S. (2016). Reduced order method for patient specific application: biomechanics of brain in presence of tumor. |
 | MAGLIULO, M., BEEX, L., ZILIAN, A., & BORDAS, S. (2016). Large-deformation lattice model for dry-woven fabrics including contact. |
 | AGATHOS, K., Chatzi, E., & BORDAS, S. (May 2016). 3D Crack Detection Using an XFEM Variant and Global Optimization Algorithms [Paper presentation]. FraMCoS 9. |
 | HAUSEUX, P., HALE, J., & BORDAS, S. (May 2016). Propagating uncertainty through a non-linear hyperelastic model using advanced Monte-Carlo methods [Paper presentation]. The FEniCS'16 workshop, Oslo, Norway. |
 | Goury, O., Amsallem, D., BORDAS, S., Liu, W. K., & Kerfriden, P. (2016). Automatised selection of load paths to construct reduced-order models in computational damage micromechanics: from dissipation-driven random selection to Bayesian optimization. Computational Mechanics. doi:10.1007/s00466-016-1290-2 Peer Reviewed verified by ORBi |
 | Peng, X., Atroshchenko, E., Kerfriden, P., & BORDAS, S. (01 April 2016). 3D fatigue fracture modeling by isogeometric boundary element methods [Paper presentation]. 24th conference on computational mechanics, UK (ACME2016). |
 | Yu, P., Claus, S., BORDAS, S., & Kerfriden, P. (01 April 2016). Error estimation and space-time adaptivity for the isogeometric analysis of transient structural dynamics [Paper presentation]. ACME Conference 2016. |
 | HALE, J., Farrel, P. E., & BORDAS, S. (2016). Bayesian statistical inference on the material parameters of a hyperelastic body. In Proceedings of the ACME-UK 2016 24th Conference on Computational Mechanics. |
 | AL-SAAD, M., Kulasegaram, S., & BORDAS, S. (31 March 2016). Blood flow simulation using smoothed particle hydrodynamics: application to thrombus generation [Paper presentation]. ACME 2016 - UK Association for Computational Methods in Engineering, Cardiff, United Kingdom. |
 | SUTULA, D., & BORDAS, S. (2016). Energy minimizing multi-crack growth in linear elastic fracture using the extended finite element method. In ACME-UK 2016 24th Conference on Computational Mechanics. Peer reviewed |
 | Peng, X., Atroshchenko, E., Kerfriden, P., & BORDAS, S. (2016). Isogeometric boundary element methods for linear elastic fracture mechanics. Cardiff University. https://orbilu.uni.lu/handle/10993/25835 |
 | RAPPEL, H., BEEX, L., HALE, J., & BORDAS, S. (04 February 2016). An introduction to Bayesian inference for material parameter identification [Paper presentation]. Kick off meeting for STOMMMAC project, Mont-Saint-Guibert, Belgium. |
 | BOURANTAS, G., & BORDAS, S. (2016). Discretization Correction Particle Strength Exchange (DC PSE) method for Linear Elasticity. University of Luxembourg. https://orbilu.uni.lu/handle/10993/27058 |
 | BEEX, L., & BORDAS, S. (2016). Discrete mechanical models and upscaling techniques for discrete materials [Poster presentation]. Computational Sciences for Medicine Workshop, Luxembourg, Luxembourg. |
Peng, X., & BORDAS, S. (2016). 2d PHT splines implementation in C++. |
Peng, X., & BORDAS, S. (2016). C++ implementation of 2D PHT splines. |
 | Schenone, E., HALE, J., BEEX, L., & BORDAS, S. (2016). Reducing non-linear PDEs using a reduced integration proper orthogonal decomposition method [Paper presentation]. FEniCS Conference 2016, Oslo, Norway. |
 | HALE, J., Farrell, P., & BORDAS, S. (2016). Using Bayesian inference to recover the material parameters of a heterogeneous hyperelastic body [Paper presentation]. 2016 European Congress on Computational Methods in Applied Sciences and Engineering, Crete, Greece. |
 | BORDAS, S. (2016). 2015 Lab report - Legato report 001. UL. https://orbilu.uni.lu/handle/10993/23314 |
 | BAROLI, D., BORDAS, S., BEEX, L., & HALE, J. (2016). Reduced order method combined with domain decomposition [Paper presentation]. Recent developments in numerical methods for model reduction. |
 | Pereira, K., BORDAS, S., TOMAR, S., Trobec, R., Depolli, M., Kosec, G., & Magd, A. W. (2016). On the convergence of stresses in fretting fatigue. Materials, 9 (8). doi:10.3390/ma9080639 Peer reviewed |
 | NGUYEN, V. H., Nguyen, C. T., BORDAS, S., & Heidarpour, A. (2016). Modelling interfacial cracking with non-matching cohesive interface elements. Computational Mechanics, 58 (5), 731-746. doi:10.1007/s00466-016-1314-y Peer reviewed |
 | BOURANTAS, G., Lavier, L., VAN DAM, T., & BORDAS, S. (2016). Hybrid mesh/particle meshless method for modeling geological flows with discontinuous transport properties. ORBilu-University of Luxembourg. https://orbilu.uni.lu/handle/10993/26773. |
 | AGATHOS, K., Chatzi, E., & BORDAS, S. (2016). Stable 3D extended finite elements with higher order enrichment for accurate non planar fracture. Computer Methods in Applied Mechanics and Engineering, 306, 19-46. doi:10.1016/j.cma.2016.03.023 Peer Reviewed verified by ORBi |
 | Hoang, K. C., Kerfriden, P., & BORDAS, S. (2016). A fast, certified and "tuning free" two-field reduced basis method for the metamodelling of affinely-parametrised elasticity problems. Computer Methods in Applied Mechanics and Engineering, 298, 121-158. doi:10.1016/j.cma.2015.08.016 Peer Reviewed verified by ORBi |
 | Haojie, L., Pierre, K., & BORDAS, S. (2015). Implementation of regularized isogeometric boundary element methods for gradient-based shape optimization in two-dimensional linear elasticity. International Journal for Numerical Methods in Engineering. Peer Reviewed verified by ORBi |
 | BORDAS, S., BEEX, L., Kerfriden, P., Paladim, D.-A., Olivier, G., Akbari, A., & RAPPEL, H. (18 November 2015). Multi-scale methods for fracture: model learning across scales, digital twinning and factors of safety [Paper presentation]. Empa's topical day on “Multiscale high-performance computational modelling”, Zürich, Switzerland. |
 | BORDAS, S., HALE, J., BEEX, L., RAPPEL, H., Kerfriden, P., Goury, O., & Akbari, A. (2015). Multi-scale methods for fracture: model learning across scales, digital twinning and factors of safety
: primer on Bayesian Inference [Paper presentation]. EMPA High-performance Multiscale-Scale Day, Dübendorf, Switzerland. |
 | HALE, J., Farrell, P., & BORDAS, S. (21 October 2015). Using Bayes' theorem to infer the material parameters of human soft tissue [Paper presentation]. Bayesian Afternoon, Ghent, Belgium. |
 | Peng, X., Atroshchenko, E., Kerfriden, P., & BORDAS, S. (2015). Isogeometric boundary element methods for three dimensional fatigue crack growth. Cardiff University. https://orbilu.uni.lu/handle/10993/22289 |
 | BEEX, L., Rokos, O., Zeman, J., & BORDAS, S. (03 September 2015). Higher-order quasicontinuum methods for elastic and dissipative lattice models: uniaxial deformation and pure bending. GAMM Mitteilungen, 38 (2), 344-368. doi:10.1002/gamm.201510018 Peer reviewed |
 | Jung, A., BEEX, L., Diebels, S., & BORDAS, S. (08 August 2015). Open-Cell Aluminium Foams with Graded Coatings as Passively Controllable Energy Absorbers. Materials and Design, 87, 36-41. doi:10.1016/j.matdes.2015.07.165 Peer reviewed |
 | BORDAS, S. (31 July 2015). Isogeometric and multi-scale fracture [Paper presentation]. Washington NAVAIR presentation, Technical Data Analysis, Inc. 3190 Fairview Park Dr. Suite 650 Falls Church, VA 22042, United States. |
 | Akbari Rahimabadi, A., Kerfriden, P., & BORDAS, S. (15 July 2015). Scale selection in nonlinear fracture mechanics of heterogeneous materials. Philosophical Magazine, 95 (28-30), 3328-3347. doi:10.1080/14786435.2015.1061716 Peer Reviewed verified by ORBi |
 | BEEX, L., Kerfriden, P., Heaney, C., & BORDAS, S. (July 2015). Quasicontinuum methods for planar beam lattices (abstract) [Paper presentation]. 13th US National Congress on Computational Mechanics, San Diego, United States. |
| HALE, J., Farrel, P. E., & BORDAS, S. (July 2015). Hyperelastic Elastography in a Large-Scale Bayesian Inversion Setting [Paper presentation]. 13th US National Congress on Computational Mechanics, San Diego, United States. |
 | Agathos, K., Chatzi, E., BORDAS, S., & Talaslidis, D. (July 2015). Extended Finite Element Method with Global Enrichment [Paper presentation]. 13th U.S. National Congress on Computational Mechanics. |
 | Brunetti, M., HALE, J., BORDAS, S., & Maurini, C. (01 July 2015). fenics-shells: a UFL-based library for simulating thin structures [Paper presentation]. FEniCS 15, London, United Kingdom. |
 | Alves Paladim, D., Kerfriden, P., Moitinho de Almeida, J. P., Chevreuil, M., & BORDAS, S. (2015). Advances in error estimation for homogenisation. In 13th U.S. National Congress on Computational Mechanics. |
 | Ziael-Rad, V., HALE, J., Maurini, C., & BORDAS, S. (July 2015). Large scale phase field model of fracture and cutting in soft tissues [Paper presentation]. 2016 European Congress on Computational Methods in Applied Sciences and Engineering, Crete, Greece. |
 | HALE, J., Farrell, P. E., & BORDAS, S. (01 July 2015). A Bayesian inversion approach to recovering material parameters in hyperelastic solids using dolfin-adjoint [Paper presentation]. FEniCS 15, London, United Kingdom. |
 | BORDAS, S., Kerfriden, P., BEEX, L., Atroshchenko, E., & Miller, K. (24 June 2015). Multi-scale fracture, model reduction, CAD and image as a model [Paper presentation]. “Advanced Problems in Mechanics” The International Conference, St-Petersburg, Russia. |
 | Agathos, K., Chatzi, E., BORDAS, S., & Talaslidis, D. (17 June 2015). XFEM with global enrichment for 3D cracks [Paper presentation]. Besançon Numerical Analysis Week, Besançon, France. |
 | Phung-Van, P., Nguyen, L. B., V. Tran, L., T.D., D., Thai, C. H., Wahab, M., BORDAS, S., & Nguyen-Xuan, H. (2015). An efficient Computational approach for control of nonlinear transient responses of smart piezoelectric composite plates. International Journal of Non-Linear Mechanics. doi:10.1016/j.ijnonlinmec.2015.06.003 Peer Reviewed verified by ORBi |
 | Nguyen, V.-P., Anitescu, C., BORDAS, S., & Rabczuk, T. (2015). Isogeometric analysis: an overview and computer implementation aspects. Mathematics and Computers in Simulation. doi:10.1016/j.matcom.2015.05.008 Peer reviewed |
 | Hossain, M. N., Xu, G., BORDAS, S., Atroshchenko, E., Peng, X., Vogel, F., & Rabczuk, T. (01 June 2015). Geometry-Independent Field approximaTion (GIFT) for spline based FEM for Linear Elasticity: a Diffpack implementation [Paper presentation]. 3rd International Conference on Isogeometric Analysis, Trondheim, Norway. |
 | Tsikourkitoudi, V., Gavriliadis, P., BOURANTAS, G., Lolas, G., BORDAS, S., & Zhang, T. (14 May 2015). Control of Flame Spray Pyrolysis synthesis of Li4Ti5O12: Experimental and Computational study [Poster presentation]. European Materials Research Society (EMRS) Spring Meeting, Lille, France. |
 | Alves Paladim, D., Natarajan, S., BORDAS, S., & Kerfriden, P. (12 May 2015). The stable GFEM. Convergence, accuracy and Diffpack implementation [Paper presentation]. Meeting at Cenaero. |
 | Sutula, D., & BORDAS, S. (12 May 2015). A tutorial on multiple crack growth and intersections with XFEM [Paper presentation]. /. |
 | P., P.-V., M., A.-W., K.M., L., BORDAS, S., & H., N.-X. (May 2015). Isogeometric analysis of functionally graded carbon nanotube-reinforced composite plates using higher-order shear deformation theory. Composite Structures, 123, 137-149. doi:10.1016/j.compstruct.2014.12.021 Peer Reviewed verified by ORBi |
 | Bui, H. P., & BORDAS, S. (May 2015). Hybrid lattice-continuum approach for medical simulations [Paper presentation]. Legato meeting, Luxembourg. |
| Peng, X., Atroshchenko, E., & BORDAS, S. (May 2015). An isogeometric boundary element method for fracture modeling [Paper presentation]. workdshop in Cenareo. |
 | SCHENONE, E., HALE, J., BEEX, L., & BORDAS, S. (16 April 2015). Reduced order methods [Paper presentation]. RUES seminar. |
 | BOURANTAS, G., Lavier, L., Claus, S., VAN DAM, T., & BORDAS, S. (12 April 2015). Hybrid mesh/particle meshless method for geological flows with discontinuous transport properties [Paper presentation]. European Geosciences Union General Assembly 2015, Vienna, Austria. |
 | MALUKHIN, K., BORDAS, S., & BILGER, A. (02 April 2015). Biological Tissue Cutting Mechanics and Dynamics [Paper presentation]. RUES Seminars at the University of Luxembourg (FSTC, Kirchberg), Luxembourg, Luxembourg. |
 | Bui, H. P., Courtecuisse, H., BORDAS, S., & Cotin, S. (06 February 2015). Real-time surgical simulation using a lattice-continuum approach [Paper presentation]. SHACRA workshop, La Bresse, France. |
 | Bui, H. P., & BORDAS, S. (February 2015). Real-time surgical simulation using a lattice-continuum approach [Paper presentation]. SHACRA workshop, La Bresse, France. |
 | Alves Paladim, D., Kerfriden, P., Moitinho de Almeida, J., & BORDAS, S. (30 January 2015). Error estimation in homogenisation [Paper presentation]. ITN Insist Workshop, Strobl, Austria. |
 | Akbari, A., Kerfriden, I., & BORDAS, S. (2015). Error Controlled Adaptive Multiscale Method For Fracture Modelling in Polycrystalline materials. Philosophical Magazine. Peer Reviewed verified by ORBi |
 | BORDAS, S. (2015). Computational Mechanics Lab Report 2013-2014. (1). University of Luxembourg. https://orbilu.uni.lu/handle/10993/19425 |
 | Hoang, K. C., Kerfriden, P., Khoo, B. C., & BORDAS, S. (2015). An efficient goal-oriented sampling strategy using reduced basis method for parametrized elastodynamic problems. Numerical Methods for Partial Differential Equations, 31 (2), 575-608. doi:10.1002/num.21932 Peer Reviewed verified by ORBi |
 | Yang, S.-W., Budarapu, P. R., Mahapatra, D. R., BORDAS, S., Zi, G., & Rabczuk, T. (2015). A meshless adaptive multiscale method for fracture. Computational Materials Science, 96 (PB), 382-395. doi:10.1016/j.commatsci.2014.08.054 Peer Reviewed verified by ORBi |
 | Agathos, K., Ventura, G., Chatzi, E., & BORDAS, S. (2015). Three-Dimensional Crack Propagation with Global Enrichment XFEM and Vector Level Sets [Paper presentation]. X-DMS 2015. |
 | Zhao, X., BORDAS, S., & Qu, J. (2015). Equilibrium morphology of misfit particles in elastically stressed solids under chemo-mechanical equilibrium conditions. Journal of the Mechanics and Physics of Solids, 81, 1-21. doi:10.1016/j.jmps.2015.04.008 Peer reviewed |
 | Sheng, M., Li, G., Shah, S., Lamb, A. R., & BORDAS, S. (2015). Enriched finite elements for branching cracks in deformable porous media. Engineering Analysis with Boundary Elements, 50, 435-446. doi:10.1016/j.enganabound.2014.09.010 Peer Reviewed verified by ORBi |
 | Ghasemi, H., Kerfriden, P., Muthu, J., Zi, G., Rabczuk, T., & BORDAS, S. (2015). Interfacial shear stress optimization in sandwich beams with polymeric core using non-uniform distribution of reinforcing ingredients. Composite Structures. doi:10.1016/j.compstruct.2014.10.005 Peer Reviewed verified by ORBi |
 | Lee, C.-K., BORDAS, S., & Kerfriden, P. (2015). Gradient Smoothing in Finite Elasticity: near-incompressibility. Cardiff, United Kingdom: Cardiff University. https://orbilu.uni.lu/handle/10993/21564 |
 | BORDAS, S., Kerfriden, P., Akbari, A., & Goury, O. (2015). Adaptive methods for multiscale fracture. International Journal of Engineering Science. Peer Reviewed verified by ORBi |
Lee, C.-K., & BORDAS, S. (2015). Nonlinear FEM code with Finite elasticity lecture note written by L.A. Mihai. |
 | Ong, T. H., Hoang, T. T. P., BORDAS, S., & Nguyen-Xuan, H. (2015). A staggered cell-centered finite element method for compressible and nearly-incompressible linear elasticity on general meshes. SIAM Journal on Numerical Analysis, 53 (4), 2051-2073. doi:10.1137/140990103 Peer reviewed |
 | Natarajan, S., BORDAS, S., & Ooi, E. T. (2015). Virtual and smoothed finite elements: A connection and its application to polygonal/polyhedral finite element methods. International Journal for Numerical Methods in Engineering, 104 (13), 1173-1199. doi:10.1002/nme.4965 Peer reviewed |
 | Thai, C. H., Nguyen-Xuan, H., BORDAS, S., Nguyen-Thanh, N., & Rabczuk, T. (2015). Isogeometric Analysis of Laminated Composite Plates Using the Higher-Order Shear Deformation Theory. Mechanics of Advanced Materials and Structures, 22 (6), 451-469. doi:10.1080/15376494.2013.779050 Peer reviewed |
 | Atroshchenko, E., & BORDAS, S. (2015). Fundamental solutions and dual boundary element methods for fracture in plane Cosserat elasticity. Proceedings of the Royal Society a-Mathematical Physical and Engineering Sciences, 471 (2179). doi:10.1098/rspa.2015.0216 Peer reviewed |
 | Ghasemi, H., Kerfriden, P., BORDAS, S., Muthu, J., Zi, G., & Rabczuk, T. (2015). Probabilistic multiconstraints optimization of cooling channels in ceramic matrix composites. Composites. Part B, Engineering, 81, 107-119. doi:10.1016/j.compositesb.2015.06.023 Peer Reviewed verified by ORBi |
 | BORDAS, S., gonzález-estrada, O. A., ródenas, J. J., Nadal, E., Kerfriden, P., & Fuenmayor, F. J. (2015). Locally equilibrated stress recovery for goal oriented error estimation in the extended finite element method. Computers and Structures. doi:10.1016/j.compstruc.2015.01.015 Peer Reviewed verified by ORBi |
 | BORDAS, S. (Ed.). (2014). Advances in Applied Mechanics. Elsevier. |
 | Shuohui, Y., HALE, J., Yu, T., Bui, T. Q., & BORDAS, S. (December 2014). Isogeometric locking-free plate element: a simple first order shear deformation theory for functionally graded plates. Composite Structures, 118, 121-138. doi:10.1016/j.compstruct.2014.07.028 Peer Reviewed verified by ORBi |
 | Lian, H., BORDAS, S., & Kerfriden, P. (December 2014). Shape optimisation with isogeometric boundary element methods [Paper presentation]. Phd viva, Cardiff, United Kingdom. |
 | BORDAS, S., Kerfriden, P., BEEX, L., HALE, J., & Atroshchenko, E. (25 November 2014). Multiscale computational mechanics: industrial applications [Paper presentation]. WORKSHOP MODELISATION & SIMULATION NUMERIQUE : Applications, Enjeux, Besoins, Interactions Laboratoires/Entreprises, Nancy, Institut Elie Cartan, France. |
 | BORDAS, S., & Kerfriden, P. (11 November 2014). Multiscale fracture across scales and time [Paper presentation]. 2014 EU-US Frontiers of Engineering Symposium, Seattle, United States. |
 | BEEX, L., Peerlings, R., Geers, M., Kerfriden, P., & BORDAS, S. (05 November 2014). Multiscale Quasicontinuum Methods for Dissipative Truss Models and Beam Networks [Paper presentation]. Solid Mechanics Seminar, Prague, Czechia. |
 | BORDAS, S., Kerfriden, P., HALE, J., BEEX, L., Atroshchenko, E., & Rabczuk, T. (November 2014). Cardiff/Luxembourg Computational Mechanics Research Group [Poster presentation]. EU-US Frontiers of Engineering, Seattle, United States - Washington. |
 | BEEX, L., BORDAS, S., RAPPEL, H., & HALE, J. (14 October 2014). Discrete Multiscale Modelling and Future Research Plans concerning Metals (presentation) [Paper presentation]. ArcelorMittal Steel Forming Network Seminar 'Numerical Methods', Metz, France. |
 | BEEX, L., BORDAS, S., RAPPEL, H., & HALE, J. (14 October 2014). Discrete Multiscale Modelling and Future Research Plans concerning Metals [Paper presentation]. ArcelorMittal Steel Forming Network Seminar 'Numerical Methods', Metz, France. |
 | Akmar, I., Lahmer, T., BEEX, L., BORDAS, S., & Rabczuk, T. (September 2014). Uncertainty quantification of dry woven fabrics: A sensitivity analysis on material properties. Composite Structures, 116, 1-17. doi:10.1016/j.compstruct.2014.04.014 Peer Reviewed verified by ORBi |
 | Lian, H., BORDAS, S., & Kerfriden, P. (2014). Shape optimisation directly from CAD: an isogeometric boundary element approach. Cardiff, United Kingdom: Cardiff University. https://orbilu.uni.lu/handle/10993/19372 |
 | Sautot, C., BORDAS, S. (Other coll.), & HALE, J. (Other coll.). (2014). Extension of 2D FEniCS implementation of Cosserat non-local elasticity to the 3D case. https://orbilu.uni.lu/handle/10993/17930 |
 | Xu, G., Atroshchenko, E., Ma, W., & BORDAS, S. (2014). Geometry-Independent Field approximaTion: CAD-Analysis Integration, geometrical exactness and adaptivity. Computer Methods in Applied Mechanics and Engineering. Peer reviewed |
 | Akbari Rahimabadi, A., Kerfriden, P., & BORDAS, S. (2014). Error controlled adaptive multiscale method for fracture in polycrystalline materials. Cardiff, United Kingdom: Cardiff University. https://orbilu.uni.lu/handle/10993/19371 |
 | Goury, O., Kerfriden, P., Liu, W. K., & BORDAS, S. (24 July 2014). A model order reduction technique for speeding up computational homogenisation [Paper presentation]. World Congress in Computational Mechanics, Barcelona, Spain. |
| Sutula, D., & BORDAS, S. (24 July 2014). Global Energy Minimization for Multi-crack Growth in Linear Elastic Fracture using the Extended Finite Element Method [Paper presentation]. 11th. World Congress on Computational Mechanics (WCCM XI), Barcelona, Spain. |
| Lee, C.-K., Mihai, L. A., Kerfriden, P., & BORDAS, S. (23 July 2014). 11th. World Congress on Computational Mechanics (WCCM XI) [Paper presentation]. 11th. World Congress on Computational Mechanics (WCCM XI), Barcelona, Spain. |
 | HALE, J., BORDAS, S., Kerfriden, P., & Juan José Ródenas, G. (2014). Parallel simulations of soft-tissue using an adaptive quadtree/octree implicit boundary finite element method. In 11th. World Congress on Computational Mechanics. Peer reviewed |
 | BORDAS, S. (20 July 2014). Global energy minimization for multi-crack growth in linear elastic fracture using the extended finite element method [Paper presentation]. 11th. World Congress on Computational Mechanics (WCCM XI), Barcelona, Spain. |
 | BEEX, L., Peerlings, R., Geers, M., Kerfriden, P., & BORDAS, S. (20 July 2014). MULTISCALE QUASICONTINUUM APPROACHES FOR DISCRETE MODELS OF FIBROUS MATERIALS SUCH AS ELECTRONIC TEXTILE AND PAPER MATERIALS [Paper presentation]. 11th World Congress on Computational Mechanics. |
 | BEEX, L., Kerfriden, P., & BORDAS, S. (July 2014). Multiscale Quasicontinuum Approaches for Planar Beam Lattices [Paper presentation]. 5th International Conference on Computational Methods. |
 | Lian, H., Simpson, R., & BORDAS, S. (July 2014). Sensitivity analysis and shape optimization using isogeomgetric boundary element methods [Paper presentation]. 11th World Congress on Computational Mechanics. |
 | Lee, C.-K., Mihai, L. A., Kerfriden, P., & BORDAS, S. (July 2014). Gradient Smoothing For Nearly Incompressible Hyperelasticity [Paper presentation]. 11th World Congress on Computational Mechanics. |
 | Paladim, D., Kerfriden, P., & BORDAS, S. (July 2014). Efficient modeling of random heterogeneous materials with an uniform probability density function [Paper presentation]. 11th World Congress on Computational Mechanics. |
 | Xu, G., Atroshchenko, E., & BORDAS, S. (2014). GEOMETRY-INDEPENDENT FIELD APPROXIMATION FOR SPLINE-BASED FINITE ELEMENT METHODS. In Proceedings of the 11th World Congress in Computational Mechanics. Peer reviewed |
 | Peng, X., Atroshchenko, E., Simpson, R., Kulasegaram, S., & BORDAS, S. (July 2014). Crack growth analysis by a NURBS-based isogeometric boundary element method [Paper presentation]. 11th World Congress on Computational Mechanics. |
 | Aifantis, E., Kerfriden, P., & BORDAS, S. (01 July 2014). Challenges Ahead For Modelling And Simulation In Mechanics: From Engineering To Medicine [Paper presentation]. Shechtman International Symposium, Cancun, Mexico. |
 | Peng, X., Atroshchenko, E., Simpson, R., Kulasegaram, S., & BORDAS, S. (July 2014). Crack growth analysis by a NURBS-based isogeometric boundary element metyhod [Paper presentation]. 11th World Congress on Computational Mechanics. |
| Lian, H., & BORDAS, S. (2014). The codes on three dimensional shape optimisation using IGABEM. |
 | BEEX, L., Peerlings, R., Geers, M., Kerfriden, P., BORDAS, S., Heaney, C., & Os, van, K. (July 2014). Multiscale quasicontinuum approaches for beam lattices [Paper presentation]. 5th International Conference on Computational Methods, Cambridge, United Kingdom. |
 | BEEX, L., Peerlings, R., Geers, M., Kerfriden, P., BORDAS, S., Heaney, C., & Os, van, K. (July 2014). Multiscale quasicontinuum methods for fibrous materials [Paper presentation]. 11th World Congress on Computational Mechanics, Barcelona, Spain. |
 | Hossain, M. N., Vogel, F., Paladim, D. A., Nguyen, V. P., & BORDAS, S. (July 2014). Implementation of an isogeometric finite element toolbox in Diffpack [Paper presentation]. 11th World Congress on Computational Mechanics. |
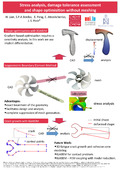 | HALE, J., BORDAS, S., Peng, X., Atroshchenko, E., & Lian, H. (24 June 2014). Stress analysis, damage tolerance assessment and shape optimisation without meshing [Poster presentation]. 1st International Workshop on Software Solutions for ICME, Rolduc Abbey, Netherlands. |
 | Kerfriden, P., Goury, O., Khac Chi, H., & BORDAS, S. (2014). A model order reduction approach to construct efficient and reliable virtual charts in computational homogenisation. In Proceedings of the 17th U.S. National Congress on Theoretical and Applied Mechanics. Peer reviewed |
 | Peng, X., Atroshchenko, E., Kulasegaram, S., & BORDAS, S. (2014). A two-dimensional isogeometric boundary element method for linear elastic fracture. Cardiff University. https://orbilu.uni.lu/handle/10993/17100 |
 | Peng, X., Atroshchenko, E., & BORDAS, S. (June 2014). Damage tolerance assessment directly from CAD: (extended) isogeometric boundary element methods [Paper presentation]. 6 international conference on advanced computational methods in engineering. |
 | HALE, J., BORDAS, S., Kerfriden, P., Ródenas García, J. J., Ortiz Benardin, A., Cyron, C. J., & Baiz, P. M. (28 May 2014). Direct image-analysis methods for surgical simulation and mixed meshfree methods [Paper presentation]. Invited seminar at Université Pierre-et-Marie-Curie, Paris, France. |
 | Bhattacharjee, K., Natarajan, S., & BORDAS, S. (2014). A hybrid T-Trefftz polygonal finite element for linear elasticity. ORBilu-University of Luxembourg. https://orbilu.uni.lu/handle/10993/16801. |
 | Kerfriden, P., Goury, O., Akbari, A., Chi, H., Rabczuk, T., Ródenas, J.-J., & BORDAS, S. (15 May 2014). Reduced order modelling: towards tractable computational homogenisation schemes [Paper presentation]. Durham Seminar Series, Durham, United Kingdom. |
 | BORDAS, S., Kerfriden, P., HALE, J., Akbari, A., Goury, O., & Lian, H. (12 May 2014). Reducing the Mesh-burden and Computational Expense in Multi-scale Free Boundary Engineering Problems [Paper presentation]. I3MS Seminar Series 20140512, Aachen, Germany. |
 | BORDAS, S., Kerfriden, P., HALE, J., Akbari, A., Goury, O., Lian, H., & Sutula, D. (23 April 2014). Model and mesh-burden reduction for multiscale fracture: applications to polycrystals, delamination and surgical simulation [Paper presentation]. Hannover Seminar, Hannover, Germany. |
 | BORDAS, S. (11 April 2014). Adaptive methods for multiscale fracture and surgical simulation
[Paper presentation]. Imperial College Mechanical Engineering Seminar, London, United Kingdom. |
 | BORDAS, S. (10 April 2014). Multiscale simulations of fracture, mesh burden reduction with applications to surgical simulation [Paper presentation]. Imperial College Mechanical Engineering Seminar, London, United Kingdom. |
 | HALE, J., BORDAS, S., & Kerfriden, P. (10 April 2014). From image to analysis: an extended finite element method to simulate the mechanical response of soft-tissue [Paper presentation]. RUES Research Seminar 2014, Luxembourg. |
| HALE, J., BORDAS, S., Kerfriden, P., & Ródenas García, J. J. (03 April 2014). An enriched quadtree/octree implicit boundary finite element method for the simulation of incompressible hyperelastic materials [Paper presentation]. 22nd ACME Conference on Computational Mechanics, Exeter, United Kingdom. |
 | BORDAS, S. (02 April 2014). Global energy minimization for multi-crack growth in linear elastic fracture using the extended finite element method [Paper presentation]. 22nd ACME Conference on Computational Mechanics. |
 | Heaney, C., Beex, L., BORDAS, S., & Kerfriden, P. (April 2014). Summation rules for higher order Quasi-continuum methods [Paper presentation]. 22nd ACME Conference on Computational Mechanics. |
| Lian, H., & BORDAS, S. (2014). matlab code of 2D nurbs-based IGABEM shape optimisation. |
 | Lian, H., BORDAS, S., & Kerfriden, P. (2014). Shape sensitivity analysis and optimization using isogeomgetric boundary element methods in two-dimensional linear elasticity. Cardiff, United Kingdom: Cardiff University. https://orbilu.uni.lu/handle/10993/16043 |
 | BORDAS, S. (2014). Discretisation, Multiscale Fracture Mechanics Problems, Cutting & Surgical Simulation: extended finite element method, meshfree methods and isogeometric analysis [Paper presentation]. University of Limerick Talk, Limerick, Ireland. |
 | Kerfriden, P., Ródenas, J.-J., & BORDAS, S. (February 2014). Certification of projection-based reduced order modelling in computational homogenisation by the Constitutive Relation Error. International Journal for Numerical Methods in Engineering, 97 (6), 395-422. doi:10.1002/nme.4588 Peer Reviewed verified by ORBi |
 | BORDAS, S., & Kerfriden, P. (2014). Adaptive multiscale simulation of material failure: applications to molecular-dynamics/continuum coupling, polycrystalline materials and Hydrogen cutting of Silicon wafers [Paper presentation]. Workshop “Multiscale simulations", Saarbrücken, Germany. |
 | BORDAS, S. (17 January 2014). Poster: Global energy minimization for multi-crack growth in linear elastic fracture using the extended finite element method [Paper presentation]. SIAM Chapter Day, Cardiff, United Kingdom. |
 | Lee, C.-K., Mihai, L. A., Kerfriden, P., & BORDAS, S. (2014). Strain smoothing technique in 3D for nearly incompressible neo-Hookean material. Cardiff School of Engineering, Cardiff University. https://orbilu.uni.lu/handle/10993/15705 |
 | Atroshchenko, E., Peng, X., Hale, J., Tomar, S., Xu, G., & BORDAS, S. (2014). Boundary Element Method with NURBS-geometry and independent field approximations in plane elasticity [Paper presentation]. 1st Pan-American Congress on Computational Mechanics. |
 | Natarajan, S., BORDAS, S., & Ean Tat, O. (2014). On the equivalence between the cell-based smoothed finite element method and the virtual element method. ORBilu-University of Luxembourg. https://orbilu.uni.lu/handle/10993/17316. |
 | Heaney, C., Kerfriden, P., & BORDAS, S. (2014). IMPROVING THE CONVERGENCE OF BOUNDS FOR EFFECTIVE ELASTIC PARAMETERS OF HETEROGENEOUS MATERIALS [Paper presentation]. 11th World Congress on Computational Mechanics (WCCM XI). |
 | Lee, C.-K., Mihai, L. A., Kerfriden, P., & BORDAS, S. (2014). Gradient Smoothing for Nearly Incompressible Hyperelasticity [Poster presentation]. SIAM Day Cardiff. |
 | Lee, C.-K., Mihai, L. A., Kerfriden, P., & BORDAS, S. (2014). Gradient Smoothing for Nearly Incompressible Hyperealsticity [Poster presentation]. SIAM Day Cardiff. |
 | Aras, R., Shen, Y., Audette, M., & BORDAS, S. (2014). Meshless Elasticity Model and Contact Mechanics-based Verification Technique. In MICCAI Computational Biomechanics for Medicine. Springer. Peer reviewed |
 | Peng, X., Atroshchenko, E., & BORDAS, S. (2014). Damage tolerance assessment directly from CAD: (extended) isogeometric boundary element methods (XIGABEM) [Paper presentation]. 6th International Conference on Advanced COmputational Methods in ENgineering. |
 | Atroshchenko, E., & BORDAS, S. (2014). Fundamental Solutions and Dual Boundary Element Method for Crack Problems in Plane Cosserat Elasticity. Proceedings of the Royal Society. Mathematical, Physical and Engineering Sciences. doi:10.1098/rspa.2015.0216 Peer Reviewed verified by ORBi |
 | Natarajan, S., Ferreira, BORDAS, S., Carrera, E., Cinefra, M., & Zenkour, A. (2014). Analysis of functionally graded material plates using triangular elements with cell-based smoothed discrete shear gap method. Mathematical Problems in Engineering, Article ID 247932, 13. doi:10.1155/2014/247932 Peer reviewed |
 | Peng, X., Kulasegaram, S., BORDAS, S., & Wu, S. (2014). An extended finite element method (XFEM) for linear elastic fracture with smooth nodal stress. Engineering Fracture Mechanics. Peer Reviewed verified by ORBi |
 | Nguyen, V.-P., Kerfriden, P., BORDAS, S., & Rabczuk, T. (2014). Isogeometric analysis suitable trivariate NURBS representation of composite panels with a new offset algorithm. Computer-Aided Design, 55, 49-63. doi:10.1016/j.cad.2014.05.004 Peer Reviewed verified by ORBi |
 | Nguyen, V., Kerfriden, P., Brino, M., BORDAS, S., & Bonisoli, E. (2014). Nitsche’s method for two and three dimensional NURBS patch coupling. Computational Mechanics, 53 (6), 1163-1182. doi:10.1007/s00466-013-0955-3 Peer Reviewed verified by ORBi |
 | Goury, O., Kerfriden, P., & BORDAS, S. (2014). Model order reduction for speeding up computational homogenisation methods of type FE2 [Paper presentation]. Group Talk, Evanston, United States. |
 | Cahill, L. M. A., Natarajan, S., BORDAS, S., O’Higgins, R. M., & McCarthy, C. T. (2014). An experimental/numerical investigation into the main driving force for crack propagation in uni-directional fibre-reinforced composite laminae. Composite Structures, 107, 119--130. doi:10.1016/j.compstruct.2013.05.039 Peer reviewed |
 | Courtecuisse, H., Allard, J., Kerfriden, P., BORDAS, S., Cotin, S., & Duriez, C. (2014). Real-time simulation of contact and cutting of heterogeneous soft-tissues. Medical Image Analysis, 18 (2), 394-410. doi:10.1016/j.media.2013.11.001 Peer reviewed |
 | Peng, X., AtroShchenko, E., Simpson, R., BORDAS, S., & Kulasegaram, S. (January 2014). A Two-Dimensional Isogeometric Boundary Element Method For Linear Elastic Fracture [Paper presentation]. IGA 2014, Austin, Texas, United States. |
 | Paladim, D., Kerfriden, P., Moitinho de Almeida, J., & BORDAS, S. (2014). Efficient modeling of random heterogeneous materials with an uniform probability density function (slides) [Paper presentation]. 11th World Congress on Computational Mechanics. |
 | Natarajan, S., Kerfriden, P., Mahapatra, D. R., & BORDAS, S. (2014). Numerical analysis of the inclusion-crack interaction by the extended finite element method. International Journal for Computational Methods in Engineering Science and Mechanics. doi:10.1080/15502287.2013.833999 Peer Reviewed verified by ORBi |
 | Nguyen, V.-P., Kerfriden, P., BORDAS, S., & Rabczuk, T. (2014). An integrated design-analysis framework for three dimensional composite panels. Computer-Aided Design. Peer Reviewed verified by ORBi |
 | Silani, M., Talebi, H., Ziaei-Rad, S., Kerfriden, P., BORDAS, S., & Rabczuk, T. (2014). Stochastic modelling of clay/epoxy nanocomposites. Composite Structures, 118, 241-249. doi:10.1016/j.compstruct.2014.07.009 Peer reviewed |
 | Kerfriden, P., Gosselet, P., Adhikari, S., BORDAS, S., & Passieux, J.-C. (2014). POD-based model order reduction for the simulation of strong nonlinear evolutions in structures: Application to damage propagation. IOP Conference Series: Materials Science and Engineering, 10 (1). doi:10.1088/1757-899X/10/1/012165 Peer reviewed |
 | Nguyen-Thanh, N., Nguyen-Xuan, H., BORDAS, S., & Rabczuk, T. (2014). Isogeometric finite element analysis using polynomial splines over hierarchical T-meshes. IOP Conference Series: Materials Science and Engineering, 10 (1). doi:10.1088/1757-899X/10/1/012238 Peer reviewed |
 | Thai, C. H. A., BORDAS, S., Ferreira, A., Rabczuk, T. E., & Nguyen-Xuan, H. A. F. (2014). Isogeometric analysis of laminated composite and sandwich plates using a new inverse trigonometric shear deformation theory. European Journal of Mechanics. A, Solids, 43, 89-108. doi:10.1016/j.euromechsol.2013.09.001 Peer Reviewed verified by ORBi |
 | Rodrigues, J. D., Natarajan, S., FERREIRA, A., Carrera, E., Cinefra, M., & BORDAS, S. (2014). Analysis of composite plates through cell-based smoothed finite element and 4-noded mixed interpolation of tensorial components techniques. Computers and Structures, 135, 83-87. doi:10.1016/j.compstruc.2014.01.011 Peer Reviewed verified by ORBi |
 | Nguyen, V.-P., Kerfriden, P., & BORDAS, S. (2014). Two- and three-dimensional isogeometric cohesive elements for composite delamination analysis. Composites. Part B, Engineering, 60, 193-212. doi:10.1016/j.compositesb.2013.12.018 Peer Reviewed verified by ORBi |
 | Nguyen-Xuan, H., Tran, L. V., Thai, C. H., Kulasegaram, S., & BORDAS, S. (2014). Isogeometric analysis of functionally graded plates using a refined plate theory. Composites. Part B, Engineering, 64, 222-234. doi:10.1016/j.compositesb.2014.04.001 Peer Reviewed verified by ORBi |
 | BEEX, L., Kerfriden, P., Rabczuk, T., & BORDAS, S. (2014). Quasicontinuum-based multiscale approaches for plate-like beam lattices experiencing in-plane and out-of-plane deformation. Computer Methods in Applied Mechanics and Engineering, 279, 348-378. doi:10.1016/j.cma.2014.06.018 Peer reviewed |
 | Nguyen, V., Kerfriden, P., Claus, S., & BORDAS, S. (2014). Nitsche’s method method for mixed dimensional analysis: conforming and non-conforming continuum-beam and continuum-plate coupling. Computer Methods in Applied Mechanics and Engineering. Peer reviewed |
 | Chen, L., Nguyen-Thanh, N., Nguyen-Xuan, H., Rabczuk, T., BORDAS, S., & Limbert, G. (2014). Explicit finite deformation analysis of isogeometric membranes. Computer Methods in Applied Mechanics and Engineering. doi:10.1016/j.cma.2014.04.015 Peer reviewed |
 | Moumnassi, M., BORDAS, S., Figueredo, R., & Sansen, P. (2014). Analysis using higher-order XFEM: implicit representation of geometrical features from a given parametric representation. Mechanics and Industry, 15 (05), 443-448. doi:10.1051/meca/2014033 Peer Reviewed verified by ORBi |
 | Sutula, D., & BORDAS, S. (2013). Global energy minimization for multiple fracture growth. Cardiff University. https://orbilu.uni.lu/handle/10993/15109 |
 | Hoang, K. C., Kerfriden, P., & BORDAS, S. (2013). Space-time reduced basis approximation and goal-oriented a posteriori error estimation for wave equation. In Theory and Application of Model Order Reduction. Peer reviewed |
 | BORDAS, S. (Ed.). (2013). Advances in Applied Mechanics. Elsevier. |
 | Peng, X., BORDAS, S., & Natarajan, S. (September 2013). smooth nodal stress in the XFEM for crack propagation simulations [Paper presentation]. Internatiaonal Conference On Extended Finite Element Methods - XFEM 2013, Lyon France. |
 | Moumnassi, M., BORDAS, S., Figueredo, R., & Sansen, P. (2013). Analysis using higher-order XFEM: Implicit representation of geometrical features from a given parametric representation. Mécanique & Industries. Peer reviewed |
 | Nguyen, V.-P., Anitescu, C., BORDAS, S., & Rabczuk, T. (2013). Isogeometric analysis: an overview and computer implementation aspects. (Unilu - University of Luxembourg, Luxembourg). |
 | Goury, O., Kerfriden, P., & BORDAS, S. (July 2013). A multiscale partitioned reduced order model applied to damage simulation [Paper presentation]. U.S. National Congress for Computational Mechanics, Raleigh,NC, United States. |
 | Lee, C.-K., Mihai, A., & BORDAS, S. (2013). The Node-Based Smoothed Finite Element Method in nonlinear elasticity. Cardiff, United Kingdom: School of Engineering, Cardiff University. https://orbilu.uni.lu/handle/10993/13848 |
 | Akbari R., A., Kerfriden, P., & BORDAS, S. (05 June 2013). An adaptive multiscale strategy to simulate fracture of composite structures [Paper presentation]. CFRAC, Prague, Czechia. |
 | BORDAS, S., Kerfriden, P., Nguyen-Xuan, H., Zhao, X., & Qu, J. (2013). Relaxing the compatibility condition in (extended) finite element methods: applications to fracture and nano-mechanics. In Actes du CSMA, Giens, 2013. Peer reviewed |
 | Abu Bakar, I. A., Kramer, O., BORDAS, S., & Rabczuk, T. (June 2013). Optimization of elastic properties and weaving patterns of woven composites. Composite Structures, 100, 575-591. doi:10.1016/j.compstruct.2012.12.043 Peer Reviewed verified by ORBi |
 | Natarajan, S., Manickam, G., & BORDAS, S. (May 2013). Supersonic flutter analysis of functionally graded material plates with cracks. Frontiers in Aerospace Engineering, 2 (2), 91--97. Peer reviewed |
 | Bui, T. Q., Rabczuk, T., González-Estrada, O. A., Natarajan, S., Valizadeh, N., & BORDAS, S. (May 2013). NURBS-based finite element analysis of functionally graded plates: Static bending, vibration, buckling and flutter. Composite Structures, 99, 309-326. doi:10.1016/j.compstruct.2012.11.008 Peer Reviewed verified by ORBi |
 | Lian, H., Simpson, R., & BORDAS, S. (03 April 2013). Stress analysis without meshing: isogeometric boundary element method. Proceedings of the ICE - Engineering and Computational Mechanics, 166 (2), 88–99. doi:10.1680/eacm.11.00024 Peer reviewed |
 | Lian, H., Simpson, R., & BORDAS, S. (25 March 2013). Sensitivity Analysis and Shape Optimisation through a T-spline Isogeometric Boundary Element Method [Paper presentation]. International Conference on Computational Mechanics, Durham, United Kingdom. |
 | Hoang, K. C., Kerfriden, P., & BORDAS, S. (2013). A goal-oriented reduced basis method for the wave equation in inverse analysis. In International Conference on Computational Mechanics CM13 Proceedings. Peer reviewed |
 | Lian, H., Simpson, R., & BORDAS, S. (March 2013). Sensitivity Analysis and Shape Optimisation through a T-spline Isogeometric Boundary Element Method [Paper presentation]. International Conference on Computational Mechanics. |
 | Simpson, R., BORDAS, S., Lian, H., & Travelyan, J. (March 2013). An isogeometric boundary element method for elastostatic analysis: 2D implementation aspects. Computers and Structures, 118, 2-12. doi:10.1016/j.compstruc.2012.12.021 Peer Reviewed verified by ORBi |
 | Lee, C.-K., Mihai, L. A., & BORDAS, S. (2013). The Node-Based Smoothed Finite Element Method in nonlinear elasticity. Cardiff University, Cardiff School of Engineering. https://orbilu.uni.lu/handle/10993/15391 |
 | Sutula, D., & BORDAS, S. (2013). Global energy minimization for all crack increment directions in the framework of XFEM. NA. https://orbilu.uni.lu/handle/10993/13879 |
 | Pattabhi, B., Robert, G., BORDAS, S., & Timon, R. (2013). An Adaptive Multiscale Method for Quasi-static Crack Growth. Computational Mechanics. doi:10.1007/s00466-013-0952-6 Peer reviewed |
 | Talebi, H., Silani, M., BORDAS, S., Kerfriden, P., & Rabczuk, T. (2013). Molecular dynamics/xfem coupling by a three-dimensional extended bridging domain with applications to dynamic brittle fracture. International Journal for Multiscale Computational Engineering, 11 (6), 527-541. doi:10.1615/IntJMultCompEng.2013005838 Peer reviewed |
 | Kerfriden, P., Schmidt, K. M., Rabczuk, T., & BORDAS, S. (2013). Statistical extraction of process zones and representative subspaces in fracture of random composites. International Journal for Multiscale Computational Engineering, 11 (3), 253-287. doi:10.1615/IntJMultCompEng.2013005939 Peer reviewed |
 | Hoang, K. C., Kerfriden, P., & BORDAS, S. (2013). Space-time goal-oriented reduced basis approximation for linear wave equation. Cardiff University. https://orbilu.uni.lu/handle/10993/11905 |
 | Amiri, F., Anitescu, C., Arroyo, M., BORDAS, S., & Rabczuk, T. (2013). XLME interpolants, a seamless bridge between XFEM and enriched meshless methods. Computational Mechanics, 1-13. doi:10.1007/s00466-013-0891-2 Peer reviewed |
 | Zhao, X., BORDAS, S., & Qu, J. (2013). A hybrid smoothed extended finite element/level set method for modeling equilibrium shapes of nano-inhomogeneities. Computational Mechanics, 1-12. doi:10.1007/s00466-013-0884-1 Peer reviewed |
 | Lian, H., Simpson, R. N., & BORDAS, S. (2013). Stress analysis without meshing: Isogeometric boundary-element method. Proceedings of the Institution of Civil Engineers: Engineering and Computational Mechanics, 166 (2), 88-99. doi:10.1680/eacm.11.00024 Peer reviewed |
 | Goury, O., Kerfriden, P., & BORDAS, S. (2013). Dealing with interfaces in partitioned model order reduction for application to nonlinear problems [Paper presentation]. International Conference on Computational Mechanics (CM13), Durham, United Kingdom. |
 | Talebi, H., Silani, M., BORDAS, S., Kerfriden, P., & Rabczuk, T. (2013). A computational library for multiscale modeling of material failure. Computational Mechanics, 1-25. doi:10.1007/s00466-013-0948-2 Peer reviewed |
 | Natarajan, S., FERREIRA, A., BORDAS, S., Carrera, E., & Cinefra, M. (2013). Analysis of composite plates by a unified formulation-cell based smoothed finite element method and field consistent elements. Composite Structures, 105, 75-81. doi:10.1016/j.compstruct.2013.04.040 Peer Reviewed verified by ORBi |
 | Hossain, M. N., Paladim, D., Vogel, F., & BORDAS, S. (2013). Implementation of a XFEM toolbox in Diffpack. In International Conference on Extended Finite Element Methods - XFEM 2013, September 11 – 13, 2013, Lyon, France. Peer reviewed |
 | Peng, Q., Crean, J., Dearden, A. K., Huang, C., Wen, X., BORDAS, S., & De, S. (2013). Defect engineering of 2D monatomic-layer materials. Modern Physics Letters B, 27 (23). doi:10.1142/S0217984913300172 Peer Reviewed verified by ORBi |
 | Rahimabadi, A. A., Natarajan, S., & BORDAS, S. (2013). Vibration of functionally graded material plates with cutouts & cracks in thermal environment. Key Engineering Materials, 560, 157-180. doi:10.4028/www.scientific.net/KEM.560.157 Peer reviewed |
 | Ródenas, J. J., Nadal, E., González-Estrada, O. A., Fuenmayor, F. J., BORDAS, S., & Pierre, K. (2013). Explicit expressions of dual loads for accurate error estimation and bounding in goal oriented adaptivity. In J. P. Moitinho de Almeida, P. Díez, C. Tiago, ... N. Parés (Eds.), Adaptive Modeling and Simulation. Proceedings of VI ADMOS 2013. Lisbon, Portugal: CINME. Peer reviewed |
 | González-Estrada, O. A., Nadal, E., Ródenas, J. J., Kerfriden, P., BORDAS, S., & Fuenmayor, F. J. (2013). Mesh adaptivity driven by goal-oriented locally equilibrated superconvergent patch recovery. Computational Mechanics, 1-20. doi:10.1007/s00466-013-0942-8 Peer reviewed |
 | González-Estrada, O. A., Natarajan, S., Ródenas, J. J., Nguyen-Xuan, H., & BORDAS, S. (2013). Efficient recovery-based error estimation for the smoothed finite element method for smooth and singular linear elasticity. Computational Mechanics, 52 (1), 37-52. doi:10.1007/s00466-012-0795-6 Peer reviewed |
 | Paladim, D., Natarajan, S., BORDAS, S., Kerfriden, P., & Vogel, F. (2013). Stable extended finite element method: Convergence, Accuracy, Properties and Diffpack implementation. In International Conference on Extended Finite Element Methods - XFEM 2013, September 11 – 13, 2013, Lyon, France. Peer reviewed |
 | Courtecuisse, H., Kerfriden, P., & BORDAS, S. (2013). Cutting in real time in corotational elasticity and perspectives on simulating cuts. Springer. doi:10.1007/978-1-4614-6351-1_1 |
 | Kerfriden, P., Goury, O., Rabczuk, T., & BORDAS, S. (2013). A partitioned model order reduction approach to rationalise computational expenses in nonlinear fracture mechanics. Computer Methods in Applied Mechanics and Engineering, 256, 169-188. doi:10.1016/j.cma.2012.12.004 Peer reviewed |
 | Scott, M. A., Simpson, R. N., Evans, J. A., Lipton, S., BORDAS, S., Hughes, T. J. R., & Sederberg, T. W. (2013). Isogeometric boundary element analysis using unstructured T-splines. Computer Methods in Applied Mechanics and Engineering, 254, 197-221. doi:10.1016/j.cma.2012.11.001 Peer reviewed |
 | Nguyen-Xuan, H., Liu, G. R., BORDAS, S., Natarajan, S., & Rabczuk, T. (2013). An adaptive singular ES-FEM for mechanics problems with singular field of arbitrary order. Computer Methods in Applied Mechanics and Engineering, 253, 252-273. doi:10.1016/j.cma.2012.07.017 Peer reviewed |
 | Wu, S., Peng, X., Zhang, W., & BORDAS, S. (2013). The virtual node polygonal element method for nonlinear thermal analysis with application to hybrid laser welding. International Journal of Heat and Mass Transfer, 67, 1247-1254. doi:10.1016/j.ijheatmasstransfer.2013.08.062 Peer Reviewed verified by ORBi |
 | Zhao, X., Duddu, R., BORDAS, S., & Qu, J. (2013). Effects of elastic strain energy and interfacial stress on the equilibrium morphology of misfit particles in heterogeneous solids. Journal of the Mechanics and Physics of Solids, 61 (6), 1433-1445. doi:10.1016/j.jmps.2013.01.012 Peer Reviewed verified by ORBi |
 | Pattabhi Ramaiah, B., Robert, G., BORDAS, S., & Timon, R. (2012). An adaptive eXtended Bridging Scale Method for crack propagation. In An adaptive eXtended Bridging Scale Method for crack propagation. Peer reviewed |
| Lee, C.-K., & BORDAS, S. (2012). The Simple Shear and Simple Tension Problems in Linear and Nonlinear Elasticity. Cardiff, United Kingdom: School of Engineering, Cardiff University. https://orbilu.uni.lu/handle/10993/14172 |
Kerfriden, P., Akbari R., A., Goury, O., & BORDAS, S. (July 2012). Addressing lack of scale separation in fracture simulations [Paper presentation]. IUTAM 2012 Symposium Fracture Phenomena in Nature and Technology, Bresia, Italy. |
 | Lian, H., Simpson, R., & BORDAS, S. (27 March 2012). Sensitivity analysis and shape optimisation with the isogeometric boundary element methods [Paper presentation]. th Proceedings of the 20 UK Conference of the Association for Computational Mechanics in Engineering. |
 | Goury, O., Kerfriden, P., Rabczuk, T., & BORDAS, S. (March 2012). ALGEBRAIC COARSE-GRAINING METHODS IN FRACTURE MECHANICS: TACKLING LOCAL LACK OF CORRELATION USING DOMAIN DECOMPOSITION [Paper presentation]. 20th UK Conference of the Association for Computational Mechanics in Engineering, Manchester, United Kingdom. |
 | Kerfriden, P., Passieux, J. C., & BORDAS, S. (2012). Local/global model order reduction strategy for the simulation of quasi-brittle fracture. International Journal for Numerical Methods in Engineering, 89 (2), 154-179. doi:10.1002/nme.3234 Peer reviewed |
 | Akbari R, A., Kerfriden, P., Rabczuk, T., & BORDAS, S. (2012). An adaptive multiscale method for fracture based on concurrent-hierarchical hybrid modelling [Paper presentation]. 20th ACME Conference, Manchester, United Kingdom. |
 | Natarajan, S., Chakraborty, S., Thangavel, M., BORDAS, S., & Rabczuk, T. (2012). Size-dependent free flexural vibration behavior of functionally graded nanoplates. Computational Materials Science, 65, 74-80. doi:10.1016/j.commatsci.2012.06.031 Peer Reviewed verified by ORBi |
 | Long, D., Guo, Z., Liu, X., Natarajan, S., & BORDAS, S. (2012). A force-based large increment method for 2D continuum solids and the mesh convergence study. AIP Conference Proceedings, 1504, 377-387. doi:10.1063/1.4771730 Peer reviewed |
 | Nadal, E., González-Estrada, O. A., Ródenas, J. J., BORDAS, S., Kerfriden, P., & Fuenmayor, F. J. (2012). Error estimation and error bounding in quantities of interest based on equilibrated recovered displacement fields. ECCOMAS 2012 - European Congress on Computational Methods in Applied Sciences and Engineering, e-Book Full Papers, 4999-5018. Peer reviewed |
 | Nadal, E., González-Estrada, O. A., Ródenas, J. J., Kerfriden, P., BORDAS, S., & Fuenmayor, F. J. (2012). Accurate error estimate in energy norm using a nearly-equilibrated kinematically-admissible displacement recovery technique. In P. M. Pimienta (Ed.), 10th World Congress on Computational Mechanics (WCCM 2012). Sao Paulo, Brazil: Escola Politécnica. Universidade de Sao Paulo. Peer reviewed |
 | González-Estrada, O. A., Nadal, E., Ródenas, J. J., Kerfriden, P., & BORDAS, S. (2012). Error estimation in quantities of interest for XFEM using recovery techniques. In Z. J. Yang (Ed.), 20th UK National Conference of the Association for Computational Mechanics in Engineering (ACME). Manchester, United Kingdom: The University of Manchester. Peer reviewed |
 | González-Estrada, O. A., Ródenas, J. J., Nadal, E., BORDAS, S., & Kerfriden, P. (2012). Equilibrated patch recovery for accurate evaluation of upper error bounds in quantities of interest. ECCOMAS Thematic Conference - ADMOS 2011: International Conference on Adaptive Modeling and Simulation, An IACM Special Interest Conference, 209-219. Peer reviewed |
 | Nadal, E., González-Estrada, O. A., Ródenas, J. J., BORDAS, S., & Fuenmayor, F. J. (2012). Error estimation and bounding in energy norm based on a displacement recovery technique. In J. Eberhardsteiner, H. Böhm, ... F. G. Rammerstorfer (Eds.), 6th European Congress on Computational Methods in Applied Sciences and Engineering (ECCOMAS 2012). Vienna, Austria: TU Wien. Peer reviewed |
 | Nadal, E., González-Estrada, O. A., Ródenas, J. J., Kerfriden, P., BORDAS, S., & Fuenmayor, F. J. (2012). Practical error bounds in energy norm based on a recovered displacement field. In P. M. Pimienta (Ed.), 10th World Congress on Computational Mechanics (WCCM 2012). Sao Paulo, Brazil: Escola Politécnica. Universidade de Sao Paulo. Peer reviewed |
 | Ródenas, J. J., Nadal, E., González-Estrada, O. A., Fuenmayor, F. J., BORDAS, S., & Kerfriden, P. (2012). Error estimation of recovered solutions in FE analysis. Higher order h-adaptive refinement strategies. In P. M. Pimienta (Ed.), 10th World Congress on Computational Mechanics (WCCM 2012). Sao Paulo, Brazil: Escola Politécnica. Universidade de Sao Paulo. Peer reviewed |
 | Nadal, E., González-Estrada, O. A., Ródenas, J. J., BORDAS, S., & Fuenmayor, F. J. (2012). Error estimation and error bounding in energy norm based on a displacement recovery technique. ECCOMAS 2012 - European Congress on Computational Methods in Applied Sciences and Engineering, e-Book Full Papers, 5042-5057. Peer reviewed |
 | González-Estrada, O. A., Ródenas, J. J., BORDAS, S., Duflot, M., Kerfriden, P., & Giner, E. (2012). On the role of enrichment and statistical admissibility of recovered fields in a posteriori error estimation for enriched finite element methods. Engineering Computations, 29 (8), 814-841. doi:10.1108/02644401211271609 Peer reviewed |
 | Nguyen-Xuan, H., NGUYEN, H. M., BORDAS, S., Rabczuk, T., & Duflot, M. (2012). A cell-based smoothed finite element method for three dimensional solid structures. KSCE Journal of Civil Engineering, 16 (7), 1230-1242. doi:10.1007/s12205-012-1515-7 Peer reviewed |
 | Lian, H., BORDAS, S., & Sevilla, R. (2012). Recent developments in CAD/analysis integration. Computational Technology Reviews, 6, 1-36. Peer reviewed |
 | Nguyen-Vinh, H., Bakar, I., Msekh, M. A., Song, J.-H., Muthu, J., Zi, G., Le, P., BORDAS, S., Simpson, R., Natarajan, S., Lahmer, T., & Rabczuk, T. (2012). Extended finite element method for dynamic fracture of piezo-electric materials. Engineering Fracture Mechanics, 92, 19-31. doi:10.1016/j.engfracmech.2012.04.025 Peer Reviewed verified by ORBi |
 | Simpson, R. N., BORDAS, S., Asenov, A., & Brown, A. R. (2012). Enriched residual free bubbles for semiconductor device simulation. Computational Mechanics, 50 (1), 119-133. doi:10.1007/s00466-011-0658-6 Peer reviewed |
 | Chen, L., Rabczuk, T., BORDAS, S., Liu, G. R., Zeng, K. Y., & Kerfriden, P. (2012). Extended finite element method with edge-based strain smoothing (ESm-XFEM) for linear elastic crack growth. Computer Methods in Applied Mechanics and Engineering, 209-212, 250-265. doi:10.1016/j.cma.2011.08.013 Peer reviewed |
 | Simpson, R. N., BORDAS, S., Trevelyan, J., & Rabczuk, T. (2012). A two-dimensional Isogeometric Boundary Element Method for elastostatic analysis. Computer Methods in Applied Mechanics and Engineering, 209-212, 87-100. doi:10.1016/j.cma.2011.08.008 Peer reviewed |
Natarajan, S., Kerfriden, P., BORDAS, S., Mahapatra, D. R., & Rabczuk, T. (June 2011). Enriched Element Free Galerkin Method for Gradient Elasticity [Paper presentation]. XFEM 2011, Cardiff, United Kingdom. |
 | Goury, O., Kerfriden, P., Margetts, L., & BORDAS, S. (June 2011). Rationalised computational time in fracture simulation: adaptive model reduction and domain decomposition [Paper presentation]. International Conference on Extended Finite Element Methods - XFEM 2011, Cardiff, United Kingdom. |
 | Natarajan, S., Baiz, P., Mahapatra, D. R., Rabczuk, T., Kerfriden, P., & BORDAS, S. (April 2011). Natural frequencies of cracked isotropic & specially orthotropic plates using the extended finite element method [Paper presentation]. 19 UK Conference of the Association for Computational Mechanics in Engineering. |
 | Menk, A., & BORDAS, S. (2011). A robust preconditioning technique for the extended finite element method. International Journal for Numerical Methods in Engineering, 85 (13), 1609-1632. doi:10.1002/nme.3032 Peer reviewed |
 | Natarajan, S., Baiz, P. M., BORDAS, S., Rabczuk, T., & Kerfriden, P. (2011). Natural frequencies of cracked functionally graded material plates by the extended finite element method. Composite Structures, 93 (11), 3082-3092. doi:10.1016/j.compstruct.2011.04.007 Peer Reviewed verified by ORBi |
 | BORDAS, S., Natarajan, S., Kerfriden, P., Augarde, C. E., Mahapatra, D. R., Rabczuk, T., & Pont, S. D. (2011). On the performance of strain smoothing for quadratic and enriched finite element approximations (XFEM/GFEM/PUFEM). International Journal for Numerical Methods in Engineering, 86 (4-5), 637-666. doi:10.1002/nme.3156 Peer reviewed |
 | Ródenas, J. J., González-Estrada, O. A., Fuenmayor, F. J., Nadal, E., & BORDAS, S. (2011). On the use of recovery techniques for accurate error estimation and error bounding in XFEM. In S. BORDAS & P. Kerfriden (Eds.), 2nd International Conference on the Extended Finite Element Method. Cardiff, UK, Unknown/unspecified: Cardiff University. Peer reviewed |
 | González-Estrada, O. A., Ródenas, J. J., Nadal, E., BORDAS, S., & Kerfriden, P. (2011). Accurate evaluation of K in XFEM using error estimation in quantities of interest based on equilibrated recovery. In S. BORDAS & P. Kerfriden (Eds.), 2nd International Conference on the Extended Finite Element Method. Cardiff, United Kingdom: Cardiff University. Peer reviewed |
 | González-Estrada, O. A., Ródenas, J. J., Nadal, E., BORDAS, S., & Kerfriden, P. (2011). Equilibrated patch recovery for accurate evaluation of upper error bounds in quantities of interest. In D. Audry, P. Díez, B. Tie, ... N. Parés (Eds.), Adaptive Modeling and Simulation. Proceedings of V ADMOS 2011. CINME. Peer reviewed |
 | Nadal, E., Ródenas, J. J., González-Estrada, O. A., BORDAS, S., & Kerfriden, P. (2011). Estimación precisa del error en magnitudes de interés mediante técnicas de recovery con equilibrio local. In Congress on Numerical Methods in Engineering. Peer reviewed |
 | González-Estrada, O. A., Ródenas, J. J., BORDAS, S., Nadal, E., Kerfriden, P., & Duflot, M. (2011). Accurate evaluation of stress intensity factors using error estimation in quantities of interest based on equilibrated recovery. In J. Oliver, M. Jirasek, O. Allix, ... N. Moës (Eds.), Computational Modeling of Fracture and Failure of Materials and Structures. Proceedings of CFRAC 2011. Barcelona, Spain: CINME. Peer reviewed |
 | González-Estrada, O. A., Ródenas, J. J., BORDAS, S., & Kerfriden, P. (2011). Enhanced recovery techniques for accurate evaluation of error estimates in FE aproximations. In O. Laghrouche, A. El Kacimi, P. Woodwaed, ... G. Medero (Eds.), 19th UK National Conference of the Association for Computational Mechanics in Engineering. Edinburgh, United Kingdom: Heriot-Watt University. Peer reviewed |
 | Baiz, P. M., Natarajan, S., BORDAS, S., Kerfriden, P., & Rabczuk, T. (2011). Linear buckling analysis of cracked plates by SFEM and XFEM. Journal of Mechanics of Material and Structures, 6 (9-10), 1213-1238. doi:10.2140/jomms.2011.6.1213 Peer reviewed |
Cahill, L., Natarajan, S., BORDAS, S., O'Higgins, R., McHugh, P., & McCarthy, C. (2011). Experimental-Numerical determination of the fracture toughness of a unidirectional composite material using DIC and a J-Integral approach [Paper presentation]. IWCMM. |
 | Thai-Hoang, C., Nguyen-Thanh, N., Nguyen-Xuan, H., Rabczuk, T., & BORDAS, S. (2011). A cell - based smoothed finite element method for free vibration and buckling analysis of shells. KSCE Journal of Civil Engineering, 15 (2), 347-361. doi:10.1007/s12205-011-1092-1 Peer reviewed |
 | Zhuang, X., Augarde, C., & BORDAS, S. (2011). Accurate fracture modelling using meshless methods, the visibility criterion and level sets: Formulation and 2D modelling. International Journal for Numerical Methods in Engineering, 86 (2), 249-268. doi:10.1002/nme.3063 Peer reviewed |
 | Dunant, C. F., BORDAS, S., Kerfriden, P., Scrivener, K. L., & Rabczuk, T. (2011). An Algorithm to compute damage from load in composites. Frontiers of Architecture and Civil Engineering in China, 5 (2), 180-193. doi:10.1007/s11709-011-0107-9 Peer reviewed |
 | Nguyen-Thanh, N., Rabczuk, T., Nguyen-Xuan, H., & BORDAS, S. (2011). An alternative alpha finite element method with discrete shear gap technique for analysis of isotropic Mindlin-Reissner plates. Finite Elements in Analysis and Design, 47 (5), 519-535. doi:10.1016/j.finel.2011.01.004 Peer reviewed |
 | Menk, A., & BORDAS, S. (2011). Crack growth calculations in solder joints based on microstructural phenomena with X-FEM. Computational Materials Science, 50 (3), 1145-1156. doi:10.1016/j.commatsci.2010.11.014 Peer Reviewed verified by ORBi |
 | Menk, A., Pearce, C. J., Lanier, O., Simpson, R., & BORDAS, S. (2011). Lifetime prediction for solder joints with the extended finite element method. Proceedings of 12th Int. Conf. on Thermal, Mechanical and Multi-Physics Simulation and Experiments in Microelectronics and Microsystems, EuroSimE 2011. doi:10.1109/ESIME.2011.5765773 Peer reviewed |
 | Vu-Bac, N., Nguyen-Xuan, H., Chen, L., BORDAS, S., Kerfriden, P., Simpson, R. N., Liu, G. R., & Rabczuk, T. (2011). A node-based smoothed extended finite element method (NS-XFEM) for fracture analysis. Computer Modeling in Engineering and Sciences, 73 (4), 331-355. doi:10.3970/cmes.2011.073.331 Peer reviewed |
 | Natarajan, S., Baiz, P. M., Ganapathi, M., Kerfriden, P., & BORDAS, S. (2011). Linear free flexural vibration of cracked functionally graded plates in thermal environment. Computers and Structures, 89 (15-16), 1535-1546. doi:10.1016/j.compstruc.2011.04.002 Peer Reviewed verified by ORBi |
 | Kerfriden, P., Gosselet, P., Adhikari, S., & BORDAS, S. (2011). Bridging proper orthogonal decomposition methods and augmented Newton-Krylov algorithms: An adaptive model order reduction for highly nonlinear mechanical problems. Computer Methods in Applied Mechanics and Engineering, 200 (5-8), 850-866. doi:10.1016/j.cma.2010.10.009 Peer reviewed |
 | Moumnassi, M., Belouettar, S., Béchet, T., BORDAS, S., Quoirin, D., & Potier-Ferry, M. (2011). Finite element analysis on implicitly defined domains: An accurate representation based on arbitrary parametric surfaces. Computer Methods in Applied Mechanics and Engineering, 200 (5-8), 774-796. doi:10.1016/j.cma.2010.10.002 Peer reviewed |
 | Nguyen-Thanh, N., Nguyen-Xuan, H., BORDAS, S., & Rabczuk, T. (2011). Isogeometric analysis using polynomial splines over hierarchical T-meshes for two-dimensional elastic solids. Computer Methods in Applied Mechanics and Engineering, 200 (21-22), 1892-1908. doi:10.1016/j.cma.2011.01.018 Peer reviewed |
 | BORDAS, S., Rabczuk, T., Ródenas, J.-J., Kerfriden, P., Moumnassi, M., & Belouettar, S. (2010). Alleviating the Mesh Burden in Computational Solid Mechanics. In Proceedings of ECT2010. Peer reviewed |
 | Baiz, P., Natarajan, S., Kerfriden, P., BORDAS, S., & Rabczuk, T. (March 2010). LINEAR BUCKLING ANALYSIS OF CRACKED ISOTROPIC PLATES USING THE EXTENDED FINITE ELEMENT METHOD [Paper presentation]. 18th UK Conference on Computational Mechanics (ACME-UK). |
 | Natarajan, S., Roy Mahapatra, D., & BORDAS, S. (2010). Integrating strong and weak discontinuities without integration subcells and example applications in an XFEM/GFEM framework. International Journal for Numerical Methods in Engineering, 83 (3), 269-294. doi:10.1002/nme.2798 Peer reviewed |
 | BORDAS, S., & Natarajan, S. (2010). On the approximation in the smoothed finite element method (SFEM) [letter to the editor]. International Journal for Numerical Methods in Engineering, 81 (5), 660-670. Peer reviewed |
Cahill, L., Natarajan, S., McCarthy, C., & BORDAS, S. (2010). Modelling of crack growth behaviour in composite materials using the extended finite element method (XFEM) [Paper presentation]. 3rd Annual Materials Ireland Conference. |
Cahill, L., Natarajan, S., McCarthy, C., BORDAS, S., & Kerfriden, P. (2010). Enriched finite elements (XFEM) for multi-crack growth simulations in orthotropic materials [Paper presentation]. IV European Conference on Computational Mechanics (ECCM), France. |
Cahill, L., Natarajan, S., McCarthy, C., & BORDAS, S. (2010). XFEM modelling of delamination in composite materials [Paper presentation]. 18th UK conference on Computational Mechanics (ACME-UK), United Kingdom. |
 | Le, C. V., Nguyen-Xuan, H., Askes, H., BORDAS, S., Rabczuk, T., & Nguyen-Vinh, H. (2010). A cell-based smoothed finite element method for kinematic limit analysis. International Journal for Numerical Methods in Engineering, 83 (12), 1651-1674. doi:10.1002/nme.2897 Peer reviewed |
 | Nguyen-Xuan, H., Rabczuk, T., Nguyen-Thanh, N., Nguyen-Thoi, T., & BORDAS, S. (2010). A node-based smoothed finite element method with stabilized discrete shear gap technique for analysis of Reissner-Mindlin plates. Computational Mechanics, 46 (5), 679-701. doi:10.1007/s00466-010-0509-x Peer reviewed |
 | Zhang, B., Liang, Y., Guo, Z., & BORDAS, S. (2010). On the structure of a new superhard hexagonal carbon phase. AIP Conference Proceedings, 1233 (PART 1), 489-493. doi:10.1063/1.3452220 Peer reviewed |
 | Nguyen-Thanh, N., Rabczuk, T., Nguyen-Xuan, H., & BORDAS, S. (2010). An alternative alpha finite element method (AαFEM) for free and forced structural vibration using triangular meshes. Journal of Computational and Applied Mathematics, 233 (9), 2112-2135. doi:10.1016/j.cam.2009.08.117 Peer reviewed |
 | Long, D., Guo, Z., Liu, X., BORDAS, S., & Zhang, L. (2010). An element nodal force-based large increment method for elastoplasticity. AIP Conference Proceedings, 1233 (PART 1), 1401-1405. doi:10.1063/1.3452111 Peer reviewed |
 | Menk, A., & BORDAS, S. (2010). Numerically determined enrichment functions for the extended finite element method and applications to bi-material anisotropic fracture and polycrystals. International Journal for Numerical Methods in Engineering, 83 (7), 805-828. doi:10.1002/nme.2858 Peer reviewed |
 | Akbari R., A., Bagri, A., BORDAS, S., & Rabczuk, T. (2010). Analysis of thermoelastic waves in a two-dimensional functionally graded materials domain by the Meshless Local Petrov-Galerkin (MLPG) method. Computer Modeling in Engineering and Sciences, 65 (1), 27-74. Peer reviewed |
 | Ahmad Akbari, R., Bagri, A., BORDAS, S., & Rabczuk, T. (2010). Analysis of thermoelastic waves in a two-dimensional functionally graded materials domain by the Meshless Local Petrov-Galerkin (MLPG) method. Computer Modeling in Engineering and Sciences, 65 (1), 27-74. doi:10.3970/cmes.2010.065.027 Peer reviewed |
 | BORDAS, S., Rabczuk, T., Hung, N.-X., Nguyen, V. P., Natarajan, S., Bog, T., Quan, D. M., & Hiep, N. V. (2010). Strain smoothing in FEM and XFEM. Computers and Structures, 88 (23-24), 1419-1443. doi:10.1016/j.compstruc.2008.07.006 Peer Reviewed verified by ORBi |
 | Rabczuk, T., BORDAS, S., & Zi, G. (2010). On three-dimensional modelling of crack growth using partition of unity methods. Computers and Structures, 88 (23-24), 1391-1411. doi:10.1016/j.compstruc.2008.08.010 Peer Reviewed verified by ORBi |
 | Rabczuk, T., Zi, G., BORDAS, S., & Nguyen-Xuan, H. (2010). A simple and robust three-dimensional cracking-particle method without enrichment. Computer Methods in Applied Mechanics and Engineering, 199 (37-40), 2437-2455. doi:10.1016/j.cma.2010.03.031 Peer reviewed |
 | Natarajan, S., BORDAS, S., & Mahapatra, D. R. (2010). On numerical integration of discontinuous approximations in partition of unity finite elements. IUTAM Bookseries, 19, 297-304. doi:10.1007/978-90-481-3771-8_30 Peer reviewed |
Natarajan, S., dal Pont, S., Hung, N.-X., Mahapatra, D. R., Rabczuk, T., & BORDAS, S. (September 2009). Numerical integration over arbitrary surfaces in partition of unity finite elements [Paper presentation]. ASME International Mechanical Engineering Congress & Exposition. |
Natarajan, S., BORDAS, S., & Rabczuk, T. (June 2009). The smoothed extended finite element method for strong discontinuities [Paper presentation]. 23rd Biennial Conference on Numerical Analysis. |
 | Natarajan, S., Mahapatra, D. R., BORDAS, S., & Guo, Z. (April 2009). A novel numerical integration technique over arbitrary polygons [Paper presentation]. 17th. UK Conference on Computational Mechanics (ACME-UK). |
 | Natarajan, S., BORDAS, S., Rabczuk, T., & Guo, Z. (April 2009). On the Smoothed eXtended Finite Element Method for Continuum [Paper presentation]. 17th. UK Conference on Computational Mechanics (ACME-UK). |
 | Natarajan, S., BORDAS, S., & Roy mahapatra, D. (2009). Numerical integration over arbitrary polygonal domains based on Schwarz-Christoffel conformal mapping. International Journal for Numerical Methods in Engineering, 80 (1), 103-134. doi:10.1002/nme.2589 Peer reviewed |
 | Hung, N.-X., BORDAS, S., & Hung, N.-D. (2009). Addressing volumetric locking and instabilities by selective integration in smoothed finite elements. Communications in Numerical Methods in Engineering, 25 (1), 19-34. doi:10.1002/cnm.1098 Peer reviewed |
 | RABCZUK, T., BEZENSEK, B., & BORDAS, S. (2009). APPLICATION OF EXTENDED ELEMENT-FREE GALERKIN METHOD TO MULTIPLE FLAWS UNDER BRITTLE FRACTURE CONDITIONS. PROCEEDINGS OF THE ASME PRESSURE VESSELS AND PIPING CONFERENCE - 2008, VOL 6, PT A AND B, 1658. Peer reviewed |
 | Menk, A., & BORDAS, S. (2009). Influence of the microstructure on the stress state of solder joints dusing thermal cycling. Proceedings of 10th International Conference on Thermal, Mechanical and Multi-Physics Simulation and Experiments in Microelectronics and Microsystems, EuroSimE 2009. doi:10.1109/ESIME.2009.4938405 Peer reviewed |
Natarajan, S., BORDAS, S., Minh, Q. D., Nguyen, H. X., Rabczuk, T., Cahill, L., & McCarthy, C. (2008). The smoothed extended finite element method. Proceedings of the 6th International Conference on Engineering Computational Technology. doi:10.1002/nme.2713 Peer reviewed |
 | Ródenas, J. J., Duflot, M., BORDAS, S., Giner, E., González-Estrada, O. A., & Fuenmayor, F. J. (2008). Comparison of recently developed recovery type discretization error estimators for the extended finite element method. In B. A. Schrefler & U. Perego (Eds.), 8th World Congress on Computational Mechanics (WCCM8). 5th.European Congress on Computational Methods in Applied Sciences and Engineering (ECCOMAS 2008). CINME. Peer reviewed |
 | Duflot, M., & BORDAS, S. (2008). A posteriori error estimation for extended finite elements by an extended global recovery. International Journal for Numerical Methods in Engineering, 76 (8), 1123-1138. doi:10.1002/nme.2332 Peer reviewed |
 | Rabczuk, T., Zi, G., BORDAS, S., & Nguyen-Xuan, H. (2008). A geometrically non-linear three-dimensional cohesive crack method for reinforced concrete structures. Engineering Fracture Mechanics, 75 (16), 4740-4758. doi:10.1016/j.engfracmech.2008.06.019 Peer Reviewed verified by ORBi |
 | BORDAS, S., Duflot, M., & Le, P. (2008). A simple error estimator for extended finite elements. Communications in Numerical Methods in Engineering, 24 (11), 961-971. doi:10.1002/cnm.1001 Peer reviewed |
 | Duddu, R., BORDAS, S., Chopp, D., & Moran, B. (2008). A combined extended finite element and level set method for biofilm growth. International Journal for Numerical Methods in Engineering, 74 (5), 848-870. doi:10.1002/nme.2200 Peer reviewed |
 | BORDAS, S., Rabczuk, T., & Zi, G. (2008). Three-dimensional crack initiation, propagation, branching and junction in non-linear materials by an extended meshfree method without asymptotic enrichment. Engineering Fracture Mechanics, 75 (5), 943-960. doi:10.1016/j.engfracmech.2007.05.010 Peer Reviewed verified by ORBi |
 | Nguyen-Xuan, H., Rabczuk, T., BORDAS, S., & Debongnie, J. F. (2008). A smoothed finite element method for plate analysis. Computer Methods in Applied Mechanics and Engineering, 197 (13-16), 1184-1203. doi:10.1016/j.cma.2007.10.008 Peer reviewed |
 | Nguyen-Thanh, N., Rabczuk, T., Nguyen-Xuan, H., & BORDAS, S. (2008). A smoothed finite element method for shell analysis. Computer Methods in Applied Mechanics and Engineering, 198 (2), 165-177. doi:10.1016/j.cma.2008.05.029 Peer reviewed |
 | Nguyen, V. P., Rabczuk, T., BORDAS, S., & Duflot, M. (2008). Meshless methods: A review and computer implementation aspects. Mathematics and Computers in Simulation, 79 (3), 763-813. doi:10.1016/j.matcom.2008.01.003 Peer reviewed |
 | BORDAS, S., Zi, G., & Rabczuk, T. (2007). Three-dimensional non-linear fracture mechanics by enriched meshfree methods without asymptotic enrichment. In Proceedings of the IUTAM Symposium on Discretization Methods for Evolving Discontinuities (pp. 21-36). Springer. doi:10.1007/978-1-4020-6530-9_2 Peer reviewed |
 | BORDAS, S., Nguyen, P. V., Dunant, C., Guidoum, A., & Nguyen-Dang, H. (2007). An extended finite element library. International Journal for Numerical Methods in Engineering, 71 (6), 703-732. doi:10.1002/nme.1966 Peer reviewed |
 | Rabczuk, T., BORDAS, S., & Zi, G. (2007). A three-dimensional meshfree method for continuous multiple-crack initiation, propagation and junction in statics and dynamics. Computational Mechanics, 40 (3), 473-495. doi:10.1007/s00466-006-0122-1 Peer reviewed |
 | BORDAS, S., Conley, J. G., Moran, B., Gray, J., & Nichols, E. (2007). A simulation-based design paradigm for complex cast components. Engineering with Computers, 23 (1), 25-37. doi:10.1007/s00366-006-0030-1 Peer reviewed |
 | BORDAS, S., Hoppe, R. H. W., & Petrova, S. I. (2007). Mechanical failure in microstructural heterogeneous materials. Lecture Notes in Computer Science, 4310 LNCS, 533-541. doi:10.1007/978-3-540-70942-8_64 Peer reviewed |
 | Dunant, C., Nguyen, V. P., Belgasmia, M., BORDAS, S., & Guidoum, A. (2007). Architecture tradeoffs of integrating a mesh generator to partition of unity enriched object-oriented finite element software. European Journal of Computational Mechanics, 16 (2), 237-258. doi:10.3166/remn.16.237-258 Peer reviewed |
 | BORDAS, S., & Duflot, M. (2007). Derivative recovery and a posteriori error estimate for extended finite elements. Computer Methods in Applied Mechanics and Engineering, 196 (35-36), 3381-3399. doi:10.1016/j.cma.2007.03.011 Peer reviewed |
 | BORDAS, S., & Moran, B. (2006). Enriched finite elements and level sets for damage tolerance assessment of complex structures. Engineering Fracture Mechanics, 73 (9), 1176-1201. doi:10.1016/j.engfracmech.2006.01.006 Peer Reviewed verified by ORBi |
 | Francis, A., Natarajan, S., Ortiz-Bernardin, A., & BORDAS, S. (n.d.). Linear smoothing over arbitrary polytopes [Paper presentation]. WCCM 2016/ APCOM 2016, Seoul, South Korea. |
 | OBEIDAT, A., & BORDAS, S. (n.d.). REMESHED SMOOTHED PARTICLE HYDRODYNAMICS PLATFORM [Poster presentation]. Luxembourg Computational Sciences for Medicine Residential Workshop, Luxembourg, Luxembourg. |
 | Murugesan, Natarajan, S., Gadyam, P., & BORDAS, S. (n.d.). Linear smoothed extended finite element method. (1). ORBilu-University of Luxembourg. https://orbilu.uni.lu/handle/10993/29330. |
 | Atroshchenko, E., Xu, G., TOMAR, S., & BORDAS, S. (n.d.). Weakening the tight coupling between geometry and simulation in isogeometric analysis: from sub- and super- geometric analysis to Geometry Independent Field approximaTion (GIFT). ORBilu-University of Luxembourg. https://orbilu.uni.lu/handle/10993/31469. |
 | Peng, X., Atroshchenko, E., Kulasegaram, S., & BORDAS, S. (n.d.). A two-dimensional isogeometric boundary element method for linear elastic fracture: a path towards damage tolerance analysis without meshing. Cardiff University. https://orbilu.uni.lu/handle/10993/17098 |
 | Francis, A., Ortiz-Bernardin, A., BORDAS, S., & Natarajan, S. (n.d.). Linear smoothed polygonal and polyhedral finite elements. ORBilu-University of Luxembourg. https://orbilu.uni.lu/handle/10993/22417. |
 | BUI, H. P., TOMAR, S., Courtecuisse, H., Audette, M., Cotin, S., & BORDAS, S. (n.d.). Controlling the Error on Target Motion through Real-time Mesh Adaptation: Applications to Deep Brain Stimulation. ORBilu-University of Luxembourg. https://orbilu.uni.lu/handle/10993/30937. |
 | Agathos, K., Chatzi, E., BORDAS, S., & Talaslidis, D. (n.d.). A well-conditioned and optimally convergent XFEM for 3D linear elastic fracture. International Journal for Numerical Methods in Engineering. doi:10.1002/nme.4982 Peer Reviewed verified by ORBi |
 | Peng, X., Kulasegaram, S., BORDAS, S., & Shengchuan, W. (n.d.). An extended finite element method with smooth nodal stress. Cardiff, United Kingdom: Cardiff University. https://orbilu.uni.lu/handle/10993/14134 |
| HAUSEUX, P., HALE, J., & BORDAS, S. (n.d.). Solving the stochastic Burgers equation with a sensitivity derivative-driven Monte Carlo method. doi:10.6084/m9.figshare.3561306 |
 | Bui, H. P., TOMAR, S., Courtecuisse, H., Cotin, S., & BORDAS, S. (n.d.). Real-time error controlled adaptive mesh refinement in surgical simulation: Application to needle insertion simulation. IEEE Transactions on Biomedical Engineering. Peer Reviewed verified by ORBi |
SUTULA, D., & BORDAS, S. (n.d.). Minimum energy multiple crack propagation. Part II: Discrete Solution with XFEM. Engineering Fracture Mechanics. doi:10.1016/j.engfracmech.2017.07.029 Peer Reviewed verified by ORBi |
SUTULA, D., & BORDAS, S. (n.d.). Minimum energy multiple crack propagation Part I: Theory. Engineering Fracture Mechanics. Peer reviewed |
 | SUTULA, D., & BORDAS, S. (n.d.). Minimum energy multiple crack propagation. Part III: XFEM computer implementation and applications. Engineering Fracture Mechanics. doi:10.1016/j.engfracmech.2017.08.004 Peer Reviewed verified by ORBi |
 | Natarajan, S., Francis, A., Atroshchenko, E., & BORDAS, S. (n.d.). A new one point quadrature rule over arbitrary star convex polygon/polyhedron. (1). ORBilu-University of Luxembourg. https://orbilu.uni.lu/handle/10993/31594. |
 | RAPPEL, H., BEEX, L., HALE, J., & BORDAS, S. (n.d.). Bayesian inference for the stochastic identification of elastoplastic material parameters: Introduction, misconceptions and insights. (v4). ORBilu-University of Luxembourg. https://orbilu.uni.lu/handle/10993/28631. |
 | Shih-Wei, Y., Pattabhi Ramaiah, B., Roy Mahapatra, D., BORDAS, S., Pierre, K., & Timon, R. (n.d.). Coarsen Graining: A Renewal Concept of Efficient Adaptivity Techniques for Multiscale Models. Computer Methods in Applied Mechanics and Engineering. Peer reviewed |
 | Introini, C., BAROLI, D., Lorenzi, S., Cammi, A., BORDAS, S., & PETERS, B. (n.d.). A mass conservative Kalman filter algorithm for thermo-computational fluid dynamics. Materials. Peer reviewed |
 | Cascio, M., BAROLI, D., Deretzsis, I., BORDAS, S., & La Magna, A. (n.d.). Coupled Molecular Dynamics and Finite Element Method: simulations of kinetics induced by field mediated interaction. Physical Review. E, Statistical, Nonlinear, and Soft Matter Physics. Peer Reviewed verified by ORBi |